题目内容
 如图,AB为圆O的直径,C为圆O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB,延长AB交DC于点E,CF⊥AB于点F.
如图,AB为圆O的直径,C为圆O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB,延长AB交DC于点E,CF⊥AB于点F.(1)求证:直线DE与⊙O相切;
(2)若EB=2,EC=4,求⊙O的半径及AC、AD的长;
(3)在(2)的条件下,求阴影部分的面积.
考点:切线的判定,扇形面积的计算
专题:
分析:(1)连接OC,证明OC⊥DC即可解决问题.
(2)首先证明AD=2DC;进而证明AF=AD,CF=CD;运用射影定理求出CF的长即可解决问题.
(3)分别求出△ABC、半圆⊙O的面积,问题即可解决.
(2)首先证明AD=2DC;进而证明AF=AD,CF=CD;运用射影定理求出CF的长即可解决问题.
(3)分别求出△ABC、半圆⊙O的面积,问题即可解决.
解答: 解:(1)连接OC;
解:(1)连接OC;
∵AD⊥DC,
∴∠DAC+∠ACD=90°;
又∵AC平分∠DAB,OA=OC,
∴∠DAC=∠CAO,∠CAO=∠ACO,
∴∠DAC=∠ACO,
∴∠ACD+∠ACO=90°,
即OC⊥DC,
∴直线DE与⊙O相切.
(2)∵EC是⊙O的切线,
∴EC2=EB•EA,而EC=4,EB=2,
∴EA=8,AB=8-2=6;
∴⊙O的半径为3.
∵AC平分∠DAE,
∴
=
,
∴
=
=
=2,
∴AD=2DC(设为x);
∵AC平分∠DAB,CD⊥AD,CF⊥AB,
∴CD=CF;
在△ADC与△AFC中,
,
∴△ADC≌△AFC(HL),
∴AF=AD=2x,BF=6-2x;
∵AB为⊙O的直径,
∴∠ACB=90°;
由射影定理得:CF2=AF•BF,
即x2=2x(6-2x),
解得:x=
,
∴AD=
;
由勾股定理得:AC2=(
)2+(
)2,
∴AC=
,
即⊙O的半径及AC、AD的长分别为3,
,
.
(3)∵S△ABC=
×6×
=
,
S半圆O=
×π×32=
,
∴S阴影=
-
.
 解:(1)连接OC;
解:(1)连接OC;∵AD⊥DC,
∴∠DAC+∠ACD=90°;
又∵AC平分∠DAB,OA=OC,
∴∠DAC=∠CAO,∠CAO=∠ACO,
∴∠DAC=∠ACO,
∴∠ACD+∠ACO=90°,
即OC⊥DC,
∴直线DE与⊙O相切.
(2)∵EC是⊙O的切线,
∴EC2=EB•EA,而EC=4,EB=2,
∴EA=8,AB=8-2=6;
∴⊙O的半径为3.
∵AC平分∠DAE,
∴
| AD |
| AE |
| DC |
| CE |
∴
| AD |
| DC |
| AE |
| EC |
| 8 |
| 4 |
∴AD=2DC(设为x);
∵AC平分∠DAB,CD⊥AD,CF⊥AB,
∴CD=CF;
在△ADC与△AFC中,
|
∴△ADC≌△AFC(HL),
∴AF=AD=2x,BF=6-2x;
∵AB为⊙O的直径,
∴∠ACB=90°;
由射影定理得:CF2=AF•BF,
即x2=2x(6-2x),
解得:x=
| 12 |
| 5 |
∴AD=
| 24 |
| 5 |
由勾股定理得:AC2=(
| 24 |
| 5 |
| 12 |
| 5 |
∴AC=
12
| ||
| 5 |
即⊙O的半径及AC、AD的长分别为3,
12
| ||
| 5 |
| 24 |
| 5 |
(3)∵S△ABC=
| 1 |
| 2 |
| 12 |
| 5 |
| 36 |
| 5 |
S半圆O=
| 1 |
| 2 |
| 9π |
| 2 |
∴S阴影=
| 9π |
| 2 |
| 36 |
| 5 |
点评:该题以圆为载体,以切线的判定、切割线定理、角平分线的性质、射影定理等几何知识点的应用为载体构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
已知a、b满足(a+2)2+|b-3|=0,则a+b=( )
| A、1 | B、-1 | C、5 | D、-5 |
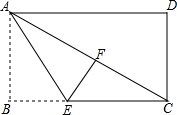 如图,在长方形ABCD中,AB=6,BC=8,先将矩形沿对角线折叠,再将矩形沿AE对折,使点B落在AC边的点F处,求折痕AE的长.
如图,在长方形ABCD中,AB=6,BC=8,先将矩形沿对角线折叠,再将矩形沿AE对折,使点B落在AC边的点F处,求折痕AE的长.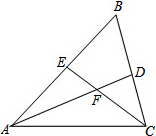 如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠ACB的角平分线,AD、CE相交于F.
如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠ACB的角平分线,AD、CE相交于F.