题目内容
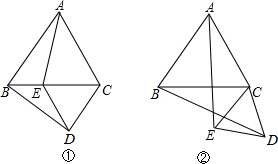
如图①,△ABC、△CDE都是等边三角形.
(1)试确定AE、BD之间的大小关系;
(2)若把△CDE绕C点按逆时针旋转到图②的位置时,上述结论仍成立吗,请说明理由.
(1)试确定AE、BD之间的大小关系;
(2)若把△CDE绕C点按逆时针旋转到图②的位置时,上述结论仍成立吗,请说明理由.

考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据等边三角形各边长相等性质可以证明△BDC≌△AEC,即可解题;
(2)易证∠ACE=∠BCD,即可求证△ACE≌△BCD,即可解题.
(2)易证∠ACE=∠BCD,即可求证△ACE≌△BCD,即可解题.
解答:解:(1)∵△ABC、△CDE都是等边三角形.
∴∠ACE=60°,∠BCD=60°,
∵在△ACE和△BCD中,
,
∴△ACE≌△BCD,(SAS),
∴AE=BD;
(2)∵△ABC、△CDE都是等边三角形.
∴∠ACB=60°,∠ECD=60°,
∴∠ACE=∠BCD,
∵在△ACE和△BCD中,
,
∴△ACE≌△BCD,(SAS),
∴AE=BD;
∴∠ACE=60°,∠BCD=60°,
∵在△ACE和△BCD中,
|
∴△ACE≌△BCD,(SAS),
∴AE=BD;
(2)∵△ABC、△CDE都是等边三角形.
∴∠ACB=60°,∠ECD=60°,
∴∠ACE=∠BCD,
∵在△ACE和△BCD中,
|
∴△ACE≌△BCD,(SAS),
∴AE=BD;
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACE≌△BCD是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
已知点A的坐标为(3,4),O为原点,连结OA,将线段OA绕点O按逆时针方向旋转90°得OA1,则点A1的坐标为( )
| A、(-3,4) |
| B、(3,-4) |
| C、(-4,3) |
| D、(4,-3) |
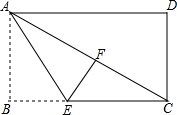 如图,在长方形ABCD中,AB=6,BC=8,先将矩形沿对角线折叠,再将矩形沿AE对折,使点B落在AC边的点F处,求折痕AE的长.
如图,在长方形ABCD中,AB=6,BC=8,先将矩形沿对角线折叠,再将矩形沿AE对折,使点B落在AC边的点F处,求折痕AE的长.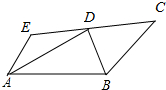 已知,如图,AE∥BC,AD、BD分别平分∠EAB、∠CBA,EC过点D.求证:AB=AE+BC.
已知,如图,AE∥BC,AD、BD分别平分∠EAB、∠CBA,EC过点D.求证:AB=AE+BC.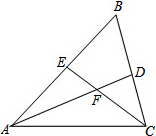 如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠ACB的角平分线,AD、CE相交于F.
如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠ACB的角平分线,AD、CE相交于F.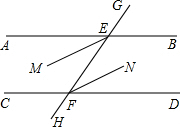 如图,已知直线AB和直线CD被直线GH所截,交点分别为E,F,∠AEF=∠EFD.
如图,已知直线AB和直线CD被直线GH所截,交点分别为E,F,∠AEF=∠EFD.