题目内容
在Rt△ABC中，∠C=90°，D为BC边（除端点外）上的一点，设∠ADC=a，∠B=b．
（1）猜想sina与sinb的大小关系；
（2）试证明你的结论．
（1）猜想sina与sinb的大小关系；
（2）试证明你的结论．
考点：解直角三角形,勾股定理
专题：
分析：（1）因为在△ABD中，∠ADC为△ABD的外角，可知∠ADC＞∠B，可猜想sina＞sinb；
（2）利用三角函数的定义可得出sina=
，sinb=
，由AD＜AB，可得出结论．
（2）利用三角函数的定义可得出sina=
| AC |
| AD |
| AC |
| AB |
解答：解：（1）猜想：sina＞sinb；
（2）证明：∵∠C=90°，
∴sina=
，sinb=
，
∵AD＜AB，
∴
＞
，
即sina＞sinb．
（2）证明：∵∠C=90°，
∴sina=
| AC |
| AD |
| AC |
| AB |
∵AD＜AB，
∴
| AC |
| AD |
| AC |
| AB |
即sina＞sinb．
点评：本题主要考查三角函数的定义，利用三角函数的定义把两角的正弦值表示成线段的比是解题的关键．
练习册系列答案
快捷英语周周练系列答案
相关题目
图中的几何体是由几个面所摆成的？面与面相交成几条线？它们是直的还是曲的？
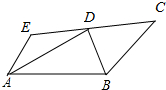已知，如图，AE∥BC，AD、BD分别平分∠EAB、∠CBA，EC过点D．求证：AB=AE+BC．
如图，AB=AC+