题目内容
14.已知A=$\root{m}{n-m+3}$是n-m+3的算术平方根,B=$\root{m-2n+3}{m+2n}$是m+2n的立方根,求B3-A2的平方根.分析 根据算术平方根和立方根的特点求出m,n的值,再代入A和B中,求出A,B,再把它代入要求的式子即可得出答案.
解答 解:∵A=$\root{m}{n-m+3}$是n-m+3的算术平方根,
∴m=2,
∵B=$\root{m-2n+3}{m+2n}$是m+2n的立方根,
∴m-2n+3=3,
∴n=1,
∴A=$\sqrt{1-2+3}$=$\sqrt{2}$,B=$\root{3}{4}$,
∴B3-A2=4-2=2,
∴B3-A2的平方根是±$\sqrt{2}$.
点评 本题主要考查了立方根和平方根,如果一个数x的立方等于a,即x的三次方等于a(x3=a),那么这个数x就叫做a的立方根;如果一个数x的平方等于a,即x的二次方等于a(x2=a,a≥0),那么这个数x就叫做a的平方根.

练习册系列答案
相关题目
9.下列说法正确的是( )
| A. | 64的立方根是±$\root{3}{64}$=±$\sqrt{4}$ | B. | -$\frac{1}{2}$是-$\frac{1}{6}$的立方根 | ||
| C. | $\root{3}{-27}$=-$\root{3}{27}$ | D. | 立方根等于它本身的数是0和1 |
3.已知MN是线段AB的垂直平分线,C,D是MN上任意两点,则∠CAD和∠CBD之间的大小关系是( )
| A. | ∠CAD<∠CBD | B. | ∠CAD=∠CBD | C. | ∠CAD>∠CBD | D. | 无法判断 |
4.下列说法正确的是( )
| A. | 相等的圆心角所对的弧相等 | B. | 平分弦的直径垂直于弦 | ||
| C. | 等弦所对的圆周角相等 | D. | 半圆所对的圆周角是直角 |
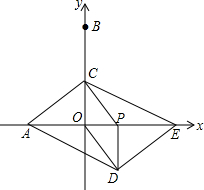 如图,在平面直角坐标系中,点A、B的坐标分别是(-2,0)、(0,4).动点P从O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止,点C停止运动时点P也随之停止运动.以CP、CO为邻边构造平行四边形PCOD,在线段OP的延长线长取点E,使得PE=2.设点P的运动时间为t秒.
如图,在平面直角坐标系中,点A、B的坐标分别是(-2,0)、(0,4).动点P从O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止,点C停止运动时点P也随之停止运动.以CP、CO为邻边构造平行四边形PCOD,在线段OP的延长线长取点E,使得PE=2.设点P的运动时间为t秒. 如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1=30°,则∠2=60°.
如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1=30°,则∠2=60°.