题目内容
13.下列计算正确的是( )| A. | $\sqrt{9}$=±3 | B. | $\sqrt{8}$-2$\sqrt{2}$=0 | C. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{(-5)^{2}}$=-5 |
分析 A、根据算术平方根的定义可知:$\sqrt{9}$=3;
B、$\sqrt{8}$可以化简为2$\sqrt{2}$,可得结果;
C、被开方数相同的最简二次根式是同类二次根式,所以$\sqrt{5}$与$\sqrt{3}$不是同类项,不能合并;
D、根据$\sqrt{{a}^{2}}$=|a|可得结果:$\sqrt{(-5)^{2}}$=5,或根据二次根式的非负性得:$\sqrt{(-5)^{2}}$≥0.
解答 解:A、$\sqrt{9}$表示9的算术平方根,值为3,所以此选项不正确;
B、$\sqrt{8}$-2$\sqrt{2}$=2$\sqrt{2}$-2$\sqrt{2}$=0,所以此选项正确;
C、$\sqrt{5}$与$\sqrt{3}$不是同类项,故$\sqrt{5}$-$\sqrt{3}$不能继续化简,所以此选项不正确;
D、$\sqrt{(-5)^{2}}$=5,所以此选项不正确;
故选B.
点评 本题考查了算术平方根的定义,熟记概念是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
8.一个盒子装有除颜色外其它均相同的2个红球和3个白球,现从中任取1个球,则取到的是一个白球的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
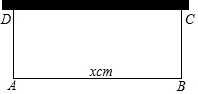 如图,用一段长为60m的篱笆围成一个一边靠墙(墙的长度不限)的长方形菜园ABCD,设与墙平行的篱笆AB的长为x m,菜园的面积为y m2.
如图,用一段长为60m的篱笆围成一个一边靠墙(墙的长度不限)的长方形菜园ABCD,设与墙平行的篱笆AB的长为x m,菜园的面积为y m2.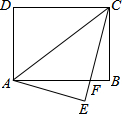 在矩形ABCD中,AB=8,BC=6,将矩形沿AC折叠后,点D落在E处,且CE与AB交于点F,求△AFC的面积.
在矩形ABCD中,AB=8,BC=6,将矩形沿AC折叠后,点D落在E处,且CE与AB交于点F,求△AFC的面积.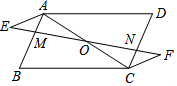 如图,四边形ABCD中,AB∥CD,BC∥DA,过AC的中点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.
如图,四边形ABCD中,AB∥CD,BC∥DA,过AC的中点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.