题目内容
2.荔枝是云南省的特色水果,小明的妈妈先购买了2千克酸味和3千克甜味,共花费90元;后又购买了1千克酸味和2千克甜味,共花费55元.(每次两种荔枝的售价都不变)(1)求酸味和甜味的售价分别是每千克多少元;
(2)如果还需购买两种荔枝共12千克,要求甜味的数量不少于酸味数量的两倍,请设计一种购买方案,使所需总费用最低.
分析 (1)设酸味售价为每千克x元,甜味售价为每千克y元,根据题意列出方程组即可解决问题.
(2)设购买酸味n千克,总费用为m元,则购买甜味12-n千克,路程不等式求出n的范围,再构建一次函数,利用一次函数的性质解决最值问题.
解答 解:(1)设酸味售价为每千克x元,甜味售价为每千克y元,
根据题意得:$\left\{\begin{array}{l}2x+3y=90\\ x+2y=55\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=15\\ y=20\end{array}\right.$
答:酸味售价为每千克15元,甜味售价为每千克20元.
(2)设购买酸味n千克,总费用为m元,则购买甜味12-n千克,
∴12-n≥2n,
∴n≤4
∴m=15n+20(12-n)=-5n+240
∵k=-5<0∴m随n的增大而减小
∴当n=4时,m=220
答:购买酸味4千克,甜味8千克时,总费用最少.
点评 本题考查一次函数的应用、二元一次方程组等知识,解题的关键是学会设未知数,列出解方程组解决问题,学会构建一次函数,利用一次函数的性质解决最值问题,属于中考常考题型.

练习册系列答案
相关题目
12.若a>b,则下列式子中错误的是( )
| A. | a-4>b-4 | B. | -4a>-4b | C. | $\frac{a}{4}$>$\frac{b}{4}$ | D. | a+n>b+n |
13.下列计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{8}$-2$\sqrt{2}$=0 | C. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{(-5)^{2}}$=-5 |
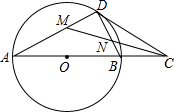 如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.
如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.
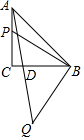 如图,△ABC是等腰直角三角形,∠C=90°,点P是直线AC上一个动点,连结BP,过点B作BQ⊥BP,且使BP=BQ,连结AQ且与直线BC相交于点D.若AP=2,AC=5,则BD的长为4或6.
如图,△ABC是等腰直角三角形,∠C=90°,点P是直线AC上一个动点,连结BP,过点B作BQ⊥BP,且使BP=BQ,连结AQ且与直线BC相交于点D.若AP=2,AC=5,则BD的长为4或6.