题目内容
18.已知:a2-4ab+5b2-2b+1=0,则以a,b为根的一元二次方程为x2-3x+2=0.分析 根据非负数的性质,求出a+b、ab的值,再由根与系数的关系,写出以a,b为根的一元二次方程即可.
解答 解:∵a2-4ab+5b2-2b+1=0,
∴a2-4ab+4b2+b2-2b+1=0,
∴(a-2b)2+(b-1)2=0,
∴a=2,b=1,
∴a+b=2,ab=1,
∴以a,b为根的一元二次方程为x2-3x+2=0.
故答案为:x2-3x+2=0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知二次函数y=ax2+bx+1(a≠0)的图象的顶点在第二象限,且过点(1,0).当a-b为整数时,ab=( )
| A. | 0 | B. | $\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | -2 |
3.若关于x的方程$\frac{x+2}{x-2}+\frac{x-2}{x+2}+\frac{4x+a}{{{x^2}-4}}=0$只有一个实数根,则符合条件的所有实数a的值的总和为( )
| A. | -6 | B. | -30 | C. | -32 | D. | -38 |
7.要证明命题“若a>b则a2>b2”是假命题,下列a,b的值能作为反例的是( )
| A. | a=-1,b=2 | B. | a=3,b=2 | C. | a=-1,b=0 | D. | a=-2,b=-1 |
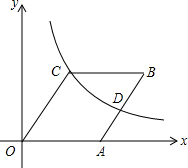 如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.
如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.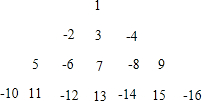 将1,-2,3,-4,5,-6…按一定规律排列如图,则第10行从左到右第9个数是-90.
将1,-2,3,-4,5,-6…按一定规律排列如图,则第10行从左到右第9个数是-90.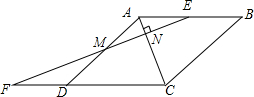 如图,四边形ABCD是菱形,点E为AB的中点,延长CD至F,使得DF=$\frac{1}{2}$CD,连接EF分别交AD,AC于点M,N.
如图,四边形ABCD是菱形,点E为AB的中点,延长CD至F,使得DF=$\frac{1}{2}$CD,连接EF分别交AD,AC于点M,N.