题目内容
8.四张质地、形状、大小完全相同的卡片,它们的正面分别写有-2,$\sqrt{3}$,$\frac{1}{2}$,π,把它们洗匀后,背面向上.(1)从中随机抽取一张卡片,是无理数的概率为$\frac{1}{2}$.
(2)小红和小丽做游戏,规则如下:先由小红随机抽出一张卡片,记下数字后不放回,再由小丽随机抽出一张卡片,记下数字,当两个数字的乘积为有理数时小红胜;当两个数字的乘积为无理数时小丽胜.请用列表法或画树状图的方法分别求出两人获胜的概率.
分析 (1)由四张质地、形状、大小完全相同的卡片,它们的正面分别写有-2,$\sqrt{3}$,$\frac{1}{2}$,π,无理数:$\sqrt{3}$,π,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两人获胜的情况,再利用概率公式即可求得答案.
解答 解:(1)∵四张质地、形状、大小完全相同的卡片,它们的正面分别写有-2,$\sqrt{3}$,$\frac{1}{2}$,π,无理数:$\sqrt{3}$,π,
∴从中随机抽取一张卡片,是无理数的概率为:$\frac{2}{4}$=$\frac{1}{2}$;
故答案为:$\frac{1}{2}$;
(2)列表得:
| 小红 | -2 | $\sqrt{3}$ | $\frac{1}{2}$ | π |
| -2 | (-2,$\sqrt{3}$) | (-2,$\frac{1}{2}$) | (-2,π) | |
| $\sqrt{3}$ | ($\sqrt{3}$,-2) | ($\sqrt{3}$,$\frac{1}{2}$) | ($\sqrt{3}$,π) | |
| $\frac{1}{2}$ | ($\frac{1}{2}$,-2) | ($\frac{1}{2}$,$\sqrt{3}$) | ($\frac{1}{2}$,π) | |
| π | (π,-2) | (π,$\sqrt{3}$) | (π,$\frac{1}{2}$) |
∴小红、小丽两人获胜的概率分别为:P(小红胜)=$\frac{2}{12}$=$\frac{1}{6}$,P(小丽胜)=$\frac{10}{12}$=$\frac{5}{6}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
3.石家庄地铁工程于2012年9月28如正式开工建设,到2020年将建成轨道交通1、2、3号线一期工程,其中1号线一期工程轨道全长约23900m,用科学记数法表示1号线一期工程的轨道全长是( )
| A. | 0.239×105m | B. | 2.39×105m | C. | 2.39×104m | D. | 23.9×103m |
13.某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示.
请你根据表中数据选一人参加比赛,最合适的人选是丁.
| 甲 | 乙 | 丙 | 丁 | |
| 平均数/环 | 9.7 | 9.5 | 9.5 | 9.7 |
| 方差/环2 | 5.1 | 4.7 | 4.5 | 4.5 |
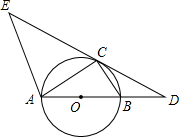 如图,AB是⊙O的直径,点C在⊙O上,∠DCB=∠CAB,AE∥BC,AE交DC的延长线于点E.
如图,AB是⊙O的直径,点C在⊙O上,∠DCB=∠CAB,AE∥BC,AE交DC的延长线于点E.