题目内容
如图所示，△EFG是由△ABC沿水平方向平移得到的，如果∠ABC＝90°，AB=3 cm，BC＝2 cm，则EF＝_________，FG=_________，EG＝_________．
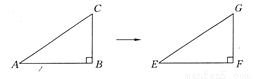
3 cm 2 cm cm
【解析】试题分析：在Rt△ABC中，AC＝＝＝（cm），
∵△EFG是由△ABC沿水平方向平移得到的，
∴EF＝AB＝3cm，FG＝BC＝2cm，EG＝AC＝cm．
故答案为3cm，2cm， cm．
练习册系列答案
相关题目
为了美化绿地，要在给定的一块长方形的空地上设计一个花坛，只允许用正方形和圆两种图形，并使整个图案成轴对称，请画出两个图形．
见解析
【解析】试题分析：根据轴对称图形的定义和题目要求画出图形即可．
试题解析：【解析】
如图所示： 如图，在四边形ABCD中，E、F分别是AB、AD的中点．若EF=2，BC=5，CD=3，则tanC等于（ ）
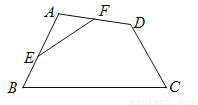
A. 
B. 
C. 
D. 
B
【解析】试题分析：连接BD．
∵E、F分別是AB、AD的中点．
∴BD=2EF=4
∵BC=5，CD=3
∴△BCD是直角三角形．
∴tanC==
故选B． 把多项式(x－2)2－4x＋8分解因式，哪一步开始出现了错误( )
【解析】
原式＝(x－2)2－(4x－8)…A
＝(x－2)2－4(x－2)…B
＝(x－2)(x－2＋4)…C
＝(x－2)(x＋2)…D
C
【解析】根据题意，第一步应是添括号（注意符号变化），解法正确，第二步先对后面因式提公因式4，再提取公因式（x-2）这时出现符号错误，所以从C步出现错误.
故选：C. 如图，这是由一个边长为a的正方形沿一条对角线的方向平移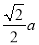
得到的图形，
① 数一数这个图案中共有几个正方形；
② 若按此方法连续做4次平移，可得怎样的图案？该图案中共有几个正方形？
3；15
【解析】试题分析：（1）根据正方形的定义即可得到答案．
（2）按此方法连续作4次平移画出图形，即可知道答案．
试题解析：
【解析】
（1）图中有3个正方形．
（2）图象如图所示，一共有15个正方形． 如图所示，下列每组图形中的两个三角形不是通过平移得到的是 ( )
A.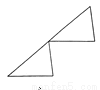 
B.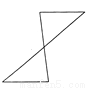 
C.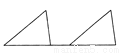 
D.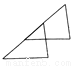 
B
【解析】试题分析：A、C、D可以通过平移得到，
B可以通过旋转得到，
故选B． 在△ABC中，高AD和BE交于H点，且BH=AC，则∠ABC=______．
45°或135°
【解析】【解析】
有2种情况．
（1）如图（1）．
∵∠BHD=∠AHE，又∠AEH=∠ADC=90°，∴∠DAC+∠C=90°，∠HAE+∠AHE=90°，
∴∠AHE=∠C，∴∠C=∠BHD．
∵BH=AC，∠HBD=∠DAC，∠C=∠BHD，∴△HBD≌△CAD，∴AD=BD．
∴∠ABC=45°；
（2）如图（2）．由（1）的解... Rt△ABC中，∠C=90°，∠B=46°，则∠A=（ ）
A. 44° B. 34° C. 54° D. 64°
A
【解析】【解析】
∵∠C=90°，∠B=46°，∴∠A=90°﹣46°=44°．故选A． 已知不等式5x+a＜3的解集与－2x+5＞1的解集相同，试求a的值．
a=－7
【解析】试题分析：先把a当作已知条件表示出x的取值范围，再根据两不等式的解集相同得出关于a的方程，求出a的值即可．
试题解析：解不等式5x+a＜3得到： .
解不等式－2x+5＞1得到：x＜2．
∵不等式5x+a＜3的解集与－2x+5＞1的解集相同，
∴=2.
解得 a=－7．