题目内容
9.解不等式组:$\left\{\begin{array}{l}{2(x-1)>3}\\{x<10-x}\end{array}\right.$,并把解集表示在数轴上.分析 先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
解答 解:不等式组:$\left\{\begin{array}{l}{2(x-1)>3①}\\{x<10-x②}\end{array}\right.$
由①得:x>$\frac{5}{2}$,
由②得:x<5
∴不等式组的解是$\frac{5}{2}$<x<5,
在数轴上表示: .
.
点评 本题主要考查对不等式的性质,解一元一次不等式(组),在数轴上表示不等式的解集等知识点的理解和掌握,能根据不等式的解集找出不等式组的解集是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.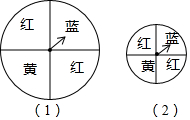 如图,两个用来摇奖的转盘,其中说法正确的是( )
如图,两个用来摇奖的转盘,其中说法正确的是( )
 如图,两个用来摇奖的转盘,其中说法正确的是( )
如图,两个用来摇奖的转盘,其中说法正确的是( )| A. | 转盘(1)中蓝色区域的面积比转盘(2)中的蓝色区域面积要大,所以摇转盘(1)比摇转盘(2)时,蓝色区域得奖的可能性大 | |
| B. | 两个转盘中指针指向蓝色区域的机会一样大 | |
| C. | 转盘(1)中,指针指向红色区域的概率是$\frac{1}{3}$ | |
| D. | 在转盘(2)中只有红、黄、蓝三种颜色,指针指向每种颜色的概率都是$\frac{1}{3}$ |


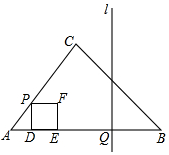 如图,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,动点P、Q同时出发,点P沿A-C-B运动,在边AC的速度为每秒1个单位长度,在边CB的速度为每秒$\sqrt{2}$个单位长度;点Q沿B-A-B以每秒2个单位长度的速度运动,其中一个动点到达终点时,另一个动点也停止运动,在运动过程中,过点P作AB的垂线与AB交于点D,以PD为边向由作正方形PDEF;过点Q作AB的垂线l.设正方形PDEF与△ABC重叠部分图形的面积为y(平方单位),运动时间为t(s).
如图,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,动点P、Q同时出发,点P沿A-C-B运动,在边AC的速度为每秒1个单位长度,在边CB的速度为每秒$\sqrt{2}$个单位长度;点Q沿B-A-B以每秒2个单位长度的速度运动,其中一个动点到达终点时,另一个动点也停止运动,在运动过程中,过点P作AB的垂线与AB交于点D,以PD为边向由作正方形PDEF;过点Q作AB的垂线l.设正方形PDEF与△ABC重叠部分图形的面积为y(平方单位),运动时间为t(s). 如图,在矩形ABCD中,AB=15,BC=8,E是AB上一点,沿DE折叠使A落在DB上,求AE的长.
如图,在矩形ABCD中,AB=15,BC=8,E是AB上一点,沿DE折叠使A落在DB上,求AE的长.