题目内容
17.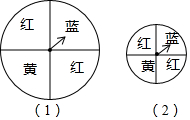 如图,两个用来摇奖的转盘,其中说法正确的是( )
如图,两个用来摇奖的转盘,其中说法正确的是( )| A. | 转盘(1)中蓝色区域的面积比转盘(2)中的蓝色区域面积要大,所以摇转盘(1)比摇转盘(2)时,蓝色区域得奖的可能性大 | |
| B. | 两个转盘中指针指向蓝色区域的机会一样大 | |
| C. | 转盘(1)中,指针指向红色区域的概率是$\frac{1}{3}$ | |
| D. | 在转盘(2)中只有红、黄、蓝三种颜色,指针指向每种颜色的概率都是$\frac{1}{3}$ |
分析 蓝色区域面积与圆盘总面积之比即为蓝色区域获奖的概率.
解答 解:由图可知(1)(2)中蓝色区域面积都是圆盘总面积的$\frac{1}{4}$.
故两个转盘中指针指向蓝色区域的机会一样大.
故选B
点评 此题考查了几何概率的计算,用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.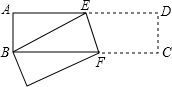 如图,已知,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )
如图,已知,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )
 如图,已知,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )
如图,已知,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | $3\sqrt{3}$ |
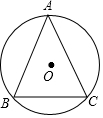 已知⊙O的半径为2,△ABC内接于⊙O,$\widehat{AB}$、$\widehat{BC}$、$\widehat{AC}$的长之比为3:2:3,求BC的长.
已知⊙O的半径为2,△ABC内接于⊙O,$\widehat{AB}$、$\widehat{BC}$、$\widehat{AC}$的长之比为3:2:3,求BC的长.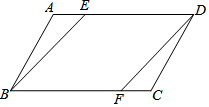 如图,ABCD是平行四边形,E、F分别是AD、BC上一点,且AE=CF.求证:EBFD是平行四边形.
如图,ABCD是平行四边形,E、F分别是AD、BC上一点,且AE=CF.求证:EBFD是平行四边形.