题目内容
19.已知a=$\sqrt{2}$+1,b=$\sqrt{2}$-1,求下列代数式的值:(1)ab
(2)a2+ab+b2
(3)$\frac{b}{a}$+$\frac{a}{b}$.
分析 (1)把a,b的值代入,根据平方差公式进行计算即可;
(2)把a2+ab+b2 化为(a+b)2-ab,再代入计算即可;
(3)先通分,再计算即可.
解答 解:(1)∵a=$\sqrt{2}$+1,b=$\sqrt{2}$-1,
∴ab=($\sqrt{2}$+1)($\sqrt{2}$-1)=2-1=1,
(2)∵a=$\sqrt{2}$+1,b=$\sqrt{2}$-1,
∴a+b=$\sqrt{2}$+1+$\sqrt{2}$-1=2$\sqrt{2}$,
∴a2+ab+b2=(a+b)2-ab=8-1=7;
(3)$\frac{b}{a}$+$\frac{a}{b}$=$\frac{{b}^{2}+{a}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$=$\frac{8-2}{1}$=6.
点评 本题考查了二次根式的化简求值,掌握完全平方公式的变形是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AB=AC,BD⊥AC于D,若∠ABC=72°,求∠ABD的度数.
如图,在△ABC中,AB=AC,BD⊥AC于D,若∠ABC=72°,求∠ABD的度数.
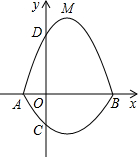 如图,在平面直角坐标系xOy中,A,B为x轴上两点,C、D为y轴上的两点,经过点A,C,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
如图,在平面直角坐标系xOy中,A,B为x轴上两点,C、D为y轴上的两点,经过点A,C,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.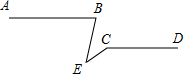 如图,AB∥CD,请探索∠B,∠C,∠E的关系?
如图,AB∥CD,请探索∠B,∠C,∠E的关系?