题目内容
5.计算:(1)a(b-a)-b(a-b)
(2)(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{201{6}^{2}}$)
分析 (1)先去括号,然后合并同类项即可解答本题;
(2)利用平方差公式可以解答本题.
解答 解:(1)a(b-a)-b(a-b)
=ab-a2-ab+b2
=-a2+b2;
(2)(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{201{6}^{2}}$)
=$(1-\frac{1}{2})(1+\frac{1}{2})(1-\frac{1}{3})(1+\frac{1}{3})(1-\frac{1}{4})(1+\frac{1}{4})…(1-\frac{1}{2016})(1+\frac{1}{2016})$
=$\frac{1}{2}×\frac{3}{2}×\frac{2}{3}×\frac{4}{3}×\frac{3}{4}×\frac{5}{4}×…×\frac{2015}{2016}×\frac{2017}{2016}$
=$\frac{1}{2}×\frac{2017}{2016}$
=$\frac{2017}{4032}$.
点评 本题考查整式的混合运算,解题的关键是明确整式的混合运算的计算方法.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
 如图,在△ABC中,D,E,F,G分别是AC,AB,ED,BF的五等分点、四等分点、三等分点,二等分点,若△ABC的面积是25,则△FGD的面积是5.
如图,在△ABC中,D,E,F,G分别是AC,AB,ED,BF的五等分点、四等分点、三等分点,二等分点,若△ABC的面积是25,则△FGD的面积是5.
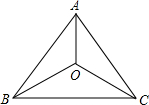 如图,在△ABC中,AB=AC.BO=CO.求证:AO⊥BC.
如图,在△ABC中,AB=AC.BO=CO.求证:AO⊥BC.