题目内容
17.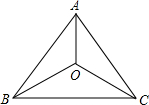 如图,在△ABC中,AB=AC.BO=CO.求证:AO⊥BC.
如图,在△ABC中,AB=AC.BO=CO.求证:AO⊥BC.
分析 延长AO交BC于点D,先证出△ABO≌△ACO,得出∠BAO=∠CAO,再根据三线合一的性质得出AO⊥BC即可.
解答 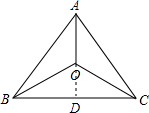 证明:延长AO交BC于点D,
证明:延长AO交BC于点D,
在△ABO和△ACO中,
$\left\{\begin{array}{l}{AB=AC}\\{AO=AO}\\{OB=OC}\end{array}\right.$,
∴△ABO≌△ACO(SSS),
∴∠BAO=∠CAO,
∵AB=AC,
∴AO⊥BC.
点评 本题考查了等腰三角形的性质,用到的知识点是全等三角形的判定和性质、等腰三角形三线合一的性质,关键是找出全等三角形.

练习册系列答案
相关题目
7. 如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )
如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )
 如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )
如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |


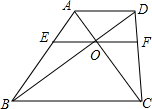 已知:如图,梯形ABCD中,AD∥BC,AC、BD交于点O,EF经过点O且和两底平行,交AB于E,交CD于F,求证:OE=OF.
已知:如图,梯形ABCD中,AD∥BC,AC、BD交于点O,EF经过点O且和两底平行,交AB于E,交CD于F,求证:OE=OF. 校园小记者就“端午节”知识随机采访了学校50名学生的情况统计图如下:A表示只知道吃粽子,B表示知道吃粽子和纪念屈原,C表示知道吃粽子、纪念屈原和悬挂药材驱瘟病,D表示知道吃粽子、纪念屈原、悬挂药材驱瘟病和赛龙舟.
校园小记者就“端午节”知识随机采访了学校50名学生的情况统计图如下:A表示只知道吃粽子,B表示知道吃粽子和纪念屈原,C表示知道吃粽子、纪念屈原和悬挂药材驱瘟病,D表示知道吃粽子、纪念屈原、悬挂药材驱瘟病和赛龙舟.