题目内容
20.已知a、b、c是△ABC的三条边,方程(b+c)x2+$\sqrt{2}$(a-c)x-$\frac{3}{4}$(a-c)=0有两个相等的实数根.试判断△ABC的形状.分析 由根的判别式△=[$\sqrt{2}$(a-c)]2-4(b+c)[-$\frac{3}{4}$(a-c)]=0,整理得出(a-c)(2a+3b+c)=0,得出a=c,判定△ABC的形状即可.
解答 解:∵方程(b+c)x2+$\sqrt{2}$(a-c)x-$\frac{3}{4}$(a-c)=0有两个相等的实数根,
∴△=[$\sqrt{2}$(a-c)]2-4(b+c)[-$\frac{3}{4}$(a-c)]=0,
∴(a-c)(2a+3b+c)=0,
∵a、b、c是△ABC的三条边,
∴a-c=0,a=c,
∴△ABC是等腰三角形.
点评 此题考查了一元二次方程根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根,关键是根据判别式和已知条件求出a,b,c的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么AC与DF平行吗?说明你的理由.
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么AC与DF平行吗?说明你的理由.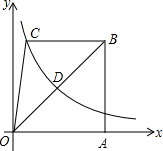 如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线y=$\frac{k}{x}$交OB于D,且OD:DB=1:2.若△OBC的面积等于8,则k的值为2.
如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线y=$\frac{k}{x}$交OB于D,且OD:DB=1:2.若△OBC的面积等于8,则k的值为2.