题目内容
9.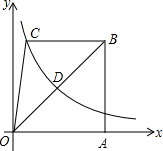 如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线y=$\frac{k}{x}$交OB于D,且OD:DB=1:2.若△OBC的面积等于8,则k的值为2.
如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线y=$\frac{k}{x}$交OB于D,且OD:DB=1:2.若△OBC的面积等于8,则k的值为2.
分析 首先过D点作DE⊥OA于E点,设C(x,y),BC=a,根据DE∥AB得比例线段表示点D坐标,根据△OBC的面积等于8得关系式.
解答 解:过D点作DE⊥OA于E点.
设C(x,y),BC=a.
则AB=y,OA=x+a.
∵OD:DB=1:2,DE∥AB,
∴△ODE∽△OBA,OD:OB=1:3,
∴DE=$\frac{1}{3}$AB=$\frac{1}{3}$y,OE=$\frac{1}{3}$OA=$\frac{1}{3}$(x+a).
∵D点在反比例函数的图象上,且D($\frac{1}{3}$(x+a),$\frac{1}{3}$y),
∴$\frac{1}{3}$y•$\frac{1}{3}$(x+a)=k,即xy+ya=9k,
∵C点在反比例函数的图象上,则xy=k,
∴ya=8k.
∵△OBC的面积等于8,
∴$\frac{1}{2}$ay=8,即ay=16.
∴8k=16,
则k=2.
故答案是:2.
点评 此题考查了反比例函数的应用、平行线分线段成比例及有关图形面积的综合运用,综合性较强,正确利用a和x表示出D的坐标是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

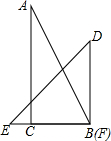 一副直角三角板按如图所示摆放一起,使等腰三角板DEF的直角顶点F与另一块直角三角板ABC的锐角顶点B(∠B=60°)重合,直角边BC与EF重合,此时两块直角三角板的斜边AB与DE的夹角(夹角指锐角或直角)是75°.
一副直角三角板按如图所示摆放一起,使等腰三角板DEF的直角顶点F与另一块直角三角板ABC的锐角顶点B(∠B=60°)重合,直角边BC与EF重合,此时两块直角三角板的斜边AB与DE的夹角(夹角指锐角或直角)是75°.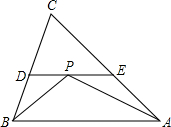 如图,△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC,AC于点D,E.
如图,△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC,AC于点D,E.