题目内容
17.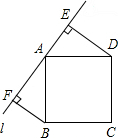 如图,直线l经过正方形ABCD的顶点A,分别过点B、D作DE⊥l于点E,BF⊥l于点F,若DE=4,BF=5,则EF的长为9.
如图,直线l经过正方形ABCD的顶点A,分别过点B、D作DE⊥l于点E,BF⊥l于点F,若DE=4,BF=5,则EF的长为9.
分析 只要证明△DAE≌△ABF得AF=DE=4,AE=BF=5,由此即可解决问题.
解答 解: ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∵∠BAF+∠DAF=90°,∠DAF+∠ADF=90°,
∴∠BAF=∠ADE,
∵BF⊥EF,DE⊥EF,
∴∠AFB=∠AED,
在△DAE和△ABF中,
$\left\{\begin{array}{l}{∠AED=∠AFB}\\{∠BAF=∠ADE}\\{AD=AB}\end{array}\right.$,
∴△DAE≌△ABF,
∴AF=DE=4,AE=BF=5,
∴EF=AF+AE=4+5=9.
故答案为9.
点评 本题考查全等三角形的判定和性质、正方形的性质等知识,解题的关键是正确寻找全等三角形,学会利用等角的余角相等证明角相等,属于中考常考题型.

练习册系列答案
相关题目
5.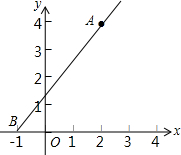 如图,已知∠α的一边在x轴上,另一边经过点A(2,4),顶点为(-1,0),则sinα的值是( )
如图,已知∠α的一边在x轴上,另一边经过点A(2,4),顶点为(-1,0),则sinα的值是( )
 如图,已知∠α的一边在x轴上,另一边经过点A(2,4),顶点为(-1,0),则sinα的值是( )
如图,已知∠α的一边在x轴上,另一边经过点A(2,4),顶点为(-1,0),则sinα的值是( )| A. | $\frac{2}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
12.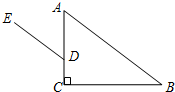 如图,在△ABC中,∠C=90°,点D在AC边上,DE∥AB,如果∠ADE=46°,那么∠B等于( )
如图,在△ABC中,∠C=90°,点D在AC边上,DE∥AB,如果∠ADE=46°,那么∠B等于( )
 如图,在△ABC中,∠C=90°,点D在AC边上,DE∥AB,如果∠ADE=46°,那么∠B等于( )
如图,在△ABC中,∠C=90°,点D在AC边上,DE∥AB,如果∠ADE=46°,那么∠B等于( )| A. | 34° | B. | 54° | C. | 46° | D. | 44° |
 如图,将正偶数按照图中所示的规律排列下去,若用有序实数对(a,b)表示第a行的第b个数.如(3,2)表示偶数10.
如图,将正偶数按照图中所示的规律排列下去,若用有序实数对(a,b)表示第a行的第b个数.如(3,2)表示偶数10.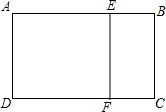 如图,矩形ABCD中,AB=6,BC=4,点E在AB上,EF⊥DC于点F,在边AD,DF,EF,AE上分别存在点M,N,P,Q,这四点构成的四边形与矩形BCFE全等,则DM的长度为$\sqrt{7}$.
如图,矩形ABCD中,AB=6,BC=4,点E在AB上,EF⊥DC于点F,在边AD,DF,EF,AE上分别存在点M,N,P,Q,这四点构成的四边形与矩形BCFE全等,则DM的长度为$\sqrt{7}$.