题目内容
5.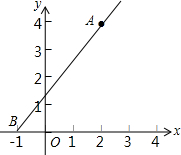 如图,已知∠α的一边在x轴上,另一边经过点A(2,4),顶点为(-1,0),则sinα的值是( )
如图,已知∠α的一边在x轴上,另一边经过点A(2,4),顶点为(-1,0),则sinα的值是( )| A. | $\frac{2}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 作AC⊥x轴于点C,根据点的坐标特征求出点A、B的坐标,得到CA、CB的长,根据勾股定理求出AB,根据正弦的定义解答即可.
解答 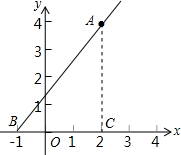 解:作AC⊥x轴于点C,
解:作AC⊥x轴于点C,
由题意得,BC=3,AC=4,
由勾股定理得,AB=5,
则sinα=$\frac{AC}{AB}$=$\frac{4}{5}$,
故选:D.
点评 本题考查的是锐角三角函数的定义,掌握在直角三角形中,一个锐角的对边比斜边是这个角的正弦,邻边比斜边是这个角的余弦,对边比邻边是这个角的正切是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
15.下列运算正确的是( )
| A. | (-x2)4=x8 | B. | a6÷a2=a3 | C. | a2+a3=a5 | D. | (-a)${\;}^{-1}=\frac{1}{a}$ |
10.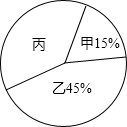 某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )
某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )
 某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )
某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图,已知甲类书有30本,则丙类书的本数是( )| A. | 80 | B. | 144 | C. | 200 | D. | 90 |
15.若关于x的一元二次方程(m-1)x2+5x+m2-3m+2=0有一个根为0,则m的值( )
| A. | 0 | B. | 1或2 | C. | 1 | D. | 2 |
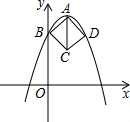 如图,在平面直角坐标系中,正方形ABCD的三个顶点A、B、D均在抛物线y=ax2-4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则AC长为4.
如图,在平面直角坐标系中,正方形ABCD的三个顶点A、B、D均在抛物线y=ax2-4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则AC长为4.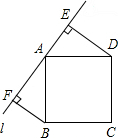 如图,直线l经过正方形ABCD的顶点A,分别过点B、D作DE⊥l于点E,BF⊥l于点F,若DE=4,BF=5,则EF的长为9.
如图,直线l经过正方形ABCD的顶点A,分别过点B、D作DE⊥l于点E,BF⊥l于点F,若DE=4,BF=5,则EF的长为9.