题目内容
7.(1)先化简,再求值:$\frac{{x}^{2}-2x}{{x}^{2}-1}$÷(x-1-$\frac{2x-1}{x+1}$),其中x=$\frac{1}{2}$(2)计算:(-2)2+2$\sqrt{12}$-8cos30°-|-3|
分析 (1)先对原式化简,然后将x=$\frac{1}{2}$代入化简后的式子即可解答本题;
(2)根据幂的乘方、特殊角的三角函数值和去绝对值可以解答本题.
解答 解:(1)$\frac{{x}^{2}-2x}{{x}^{2}-1}$÷(x-1-$\frac{2x-1}{x+1}$)
=$\frac{x(x-2)}{(x+1)(x-1)}÷\frac{(x-1)(x+1)-(2x-1)}{x+1}$
=$\frac{x(x-2)}{(x+1)(x-1)}×\frac{x+1}{{x}^{2}-1-2x+1}$
=$\frac{x(x-2)}{(x+1)(x-1)}×\frac{x+1}{x(x-2)}$
=$\frac{1}{x-1}$,
当x=$\frac{1}{2}$时,原式=$\frac{1}{\frac{1}{2}-1}=\frac{1}{-\frac{1}{2}}=-2$;
(2)(-2)2+2$\sqrt{12}$-8cos30°-|-3|
=4+$4\sqrt{3}$-8×$\frac{\sqrt{3}}{2}$-3
=4$+4\sqrt{3}-4\sqrt{3}-3$
=1.
点评 本题考查实数的运算、分式的化简求值、特殊角的三角函数值,解题的关键是明确它们各自的计算方法.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
15.下列运算正确的是( )
| A. | (-x2)4=x8 | B. | a6÷a2=a3 | C. | a2+a3=a5 | D. | (-a)${\;}^{-1}=\frac{1}{a}$ |
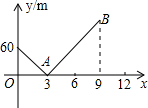 小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题:
小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题: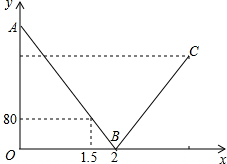 一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶80千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图象提供的信息,解答下列问题:
一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶80千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图象提供的信息,解答下列问题: 如图,E是正方形ABCD的边BC的延长线上的一点,连接AE交DC于点F 若BC=4,CE=5,求CF的长.
如图,E是正方形ABCD的边BC的延长线上的一点,连接AE交DC于点F 若BC=4,CE=5,求CF的长. 如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=4,DB=5,求阴影部分的面积.
如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=4,DB=5,求阴影部分的面积.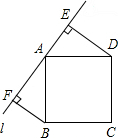 如图,直线l经过正方形ABCD的顶点A,分别过点B、D作DE⊥l于点E,BF⊥l于点F,若DE=4,BF=5,则EF的长为9.
如图,直线l经过正方形ABCD的顶点A,分别过点B、D作DE⊥l于点E,BF⊥l于点F,若DE=4,BF=5,则EF的长为9.