题目内容
10.某水果商在今年1月份用2.2万元购进A种水果和B种水果共400箱.其中A、B两种水果的数量比为5:3.已知A种水果的售价是B种水果售价的2倍少10元,预计当月即可全部售完.(1)该水果商想通过本次销售至少盈利8000元,则每箱A水果至少卖多少元?
(2)若A、B两种水果在(1)的条件下均以最低价格销售,但在实际销售中,受市场影响,A水果的销量还是下降了$\frac{8}{3}$a%,售价下降了a%;B水果的销量下降了a%,但售价不变.结果A、B两种水果的销售总额相等.求a的值.
分析 (1)设每箱B水果卖x元,则A水果每箱卖(2x-10)元,根据“A、B两种水果的总销售额-总成本≥8000”列不等式求解可得;
(2)根据“A水果下降后的销量×下降后的售价=B水果下降后的销量×售价”列出方程求解可得.
解答 解:(1)设每箱B水果卖x元,则A水果每箱卖(2x-10)元,
根据题意,得:400×$\frac{5}{8}$×(2x-10)+400×$\frac{3}{8}$x-22000≥8000,
解得:x≥50,
2x-10=100-10=90.
则A水果每箱至少卖90元,B水果每箱至少卖50元;
(2)根据题意,得:400×$\frac{5}{8}$×(1-$\frac{8}{3}$a%)×90(1-a%)=400×$\frac{3}{8}$×(1-a%)×50,
解得:a%=0.25,
则a=25.
故a的值为25.
点评 本题主要考查一元二次方程和一元一次不等式的应用,理解题意找到相等和不等关系列出方程或不等式是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
7.由多边形的一个顶点可以画8条对角线,则这个多边形的边数为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
1.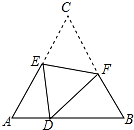 如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )
如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )
 如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )
如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )| A. | $\frac{5}{3}$ | B. | $\frac{7}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{3}{5}$ |
19. 如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
 如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )| A. | ∠A=∠D | B. | ∠ACB=∠DFE | C. | AC=DF | D. | BE=CF |
20.下列调查的样本选取方式,最具有代表性的是( )
| A. | 在青少年中调查年度最受欢迎的男歌手 | |
| B. | 了解班上学生的睡眠时间.调查班上学号为双号的学生的睡眠时间 | |
| C. | 为了了解你所在学校的学生每天的上网时间,向八年级的同学进行调查 | |
| D. | 对某市的出租司机进行体检,以此反映该市市民的健康状况 |