题目内容
1.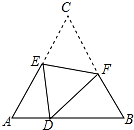 如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )
如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.25,则CE=( )| A. | $\frac{5}{3}$ | B. | $\frac{7}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{3}{5}$ |
分析 先求得AC=AB=3,由翻折的性质可知:EC=ED,然后证明△AED∽△BDF,利用相似三角形的性质可求得AE=$\frac{5}{3}$,然后可求得CE的长.
解答 解:∵△ABC为等边三角形,
∴AC=AB=3,∠A=∠B=∠C=60°.
由翻折的性质可知:∠EDF=60°.
∴∠FDB+∠EDA=120°.
∵∠EDA+∠AED=120°,
∴∠AED=∠FDB.
∴△AED∽△BDF.
∴$\frac{AE}{AD}=\frac{BD}{FB}$,即$\frac{AE}{1}$=$\frac{2}{1.25}$.
解得:AE=$\frac{8}{5}$.
CE=3-AE=3-$\frac{8}{5}$=$\frac{7}{5}$.
故选:B.
点评 本题主要考查的是等边三角形的性质、翻折的性质、相似三角形的性质和判定,利用相似三角形的性质求得AE的长是解题的关键.

练习册系列答案
相关题目
18.下列各种图形中,可以比较大小的是( )
| A. | 两条射线 | B. | 两条直线 | C. | 直线与射线 | D. | 两条线段 |
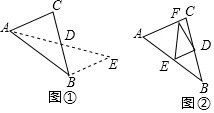
16. 把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=32°,则下列结论错误的有( )
把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=32°,则下列结论错误的有( )
 把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=32°,则下列结论错误的有( )
把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=32°,则下列结论错误的有( )| A. | ∠C′EF=32° | B. | ∠AEC=148° | C. | ∠BGE=64° | D. | ∠BFD=116° |
 (1)阅读理解:
(1)阅读理解: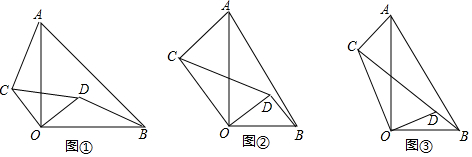
 如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )



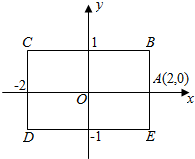 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是( )