题目内容
5.如图,直线L是一条河,P,Q是两个村庄,欲在l上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( )| A. | 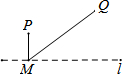 | B. | 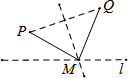 | C. | 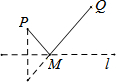 | D. | 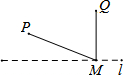 |
分析 利用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.
解答  解:作点P关于直线l的对称点P′,连接QP′交直线l于M.
解:作点P关于直线l的对称点P′,连接QP′交直线l于M.
根据两点之间,线段最短,可知选项C铺设的管道,则所需管道最短.
故选:C.
点评 本题考查了最短路径的数学问题.这类问题的解答依据是“两点之间,线段最短”.由于所给的条件的不同,解决方法和策略上又有所差别.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.在菱形ABCD中,AB=4,∠A=60°,E为AB的中点,若在线段BD上取一点P,则PA+PE的最小值是( )
| A. | 2$\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{7}$ |
15.观察下列4个命题:其中真命题是( )
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)直角三角形两锐角互余;
(4)相等的角是对顶角.
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)直角三角形两锐角互余;
(4)相等的角是对顶角.
| A. | (1)(2) | B. | (2)(3) | C. | (2)(4) | D. | (3)(4) |
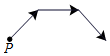
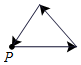
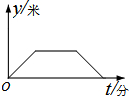 李阿姨每天早晨从家慢跑道小区公园,锻炼一阵后,再慢跑回家.表示李阿姨离开家的距离y (单位:米)与时间t (单位:分)的函数关系的图象大致如上图所示,则李阿姨跑步的路线可能是(用P点表示李阿姨家的位置)( )
李阿姨每天早晨从家慢跑道小区公园,锻炼一阵后,再慢跑回家.表示李阿姨离开家的距离y (单位:米)与时间t (单位:分)的函数关系的图象大致如上图所示,则李阿姨跑步的路线可能是(用P点表示李阿姨家的位置)( )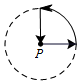
 如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )



