题目内容

19．如图，在△ABC和△DEF中，AB=DE，∠B=∠DEF，补充下列哪一条件后，能应用“SAS”判定△ABC≌△DEF（　　）
A．∠A=∠DB．∠ACB=∠DFEC．AC=DFD．BE=CF

分析 应用（SAS）从∠B的两边是AB、BC，∠E的两边是DE、EF分析，找到需要相等的两边．

解答 解：两边和它们的夹角对应相等的两个三角形全等（SAS）．∠B的两边是AB、BC，∠E的两边是DE、EF，而BC=BE+EC、EF=EC+CF，要使BC=EF，则BE=CF．
故选D．

点评 本题考查了三角形全等的条件，判定三角形全等一定要结合图形上的位置关系，从而选择方法．

练习册系列答案
相关题目
16．把一张对边互相平行的纸条，折成如图所示，EF是折痕．若∠EFB=32°，则下列结论错误的有（　　）
A．∠C′EF=32°B．∠AEC=148°C．∠BGE=64°D．∠BFD=116°
10．某水果商在今年1月份用2.2万元购进A种水果和B种水果共400箱．其中A、B两种水果的数量比为5：3．已知A种水果的售价是B种水果售价的2倍少10元，预计当月即可全部售完．
（1）该水果商想通过本次销售至少盈利8000元，则每箱A水果至少卖多少元？
（2）若A、B两种水果在（1）的条件下均以最低价格销售，但在实际销售中，受市场影响，A水果的销量还是下降了$\frac{8}{3}$a%，售价下降了a%；B水果的销量下降了a%，但售价不变．结果A、B两种水果的销售总额相等．求a的值．
7．点P1（x1，y1）、P2（x2，y2）是一次函数y=-4x+3图象上的两点，当x1＜x2＜0时，则y1与y2的大小关系是（　　）
A．y1＞y2B．y1＜y2C．y1＜y2＜0D．y1＞y2＞0
14．在菱形ABCD中，AB=4，∠A=60°，E为AB的中点，若在线段BD上取一点P，则PA+PE的最小值是（　　）
A．2$\sqrt{3}$B．4C．2$\sqrt{5}$D．2$\sqrt{7}$
4．图中，∠1和∠2是同位角的是（　　）
A．B．C．D．
11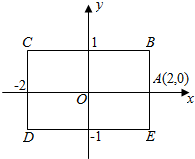．如图，矩形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙由点A（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2017次相遇地点的坐标是（　　）
A．（2，0）B．（-1，1）C．（-2，1）D．（-1，-1）
8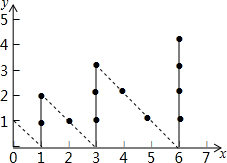．如图，一个实心点从原点出发，沿下列路径（0，0）→（0，1）→（1，0）→（1，1）→（1，2）→…每次运动一个点，则运动到第2017次时实心点所在位置的横坐标为（　　）
A．45B．946C．990D．1035
9．若64x2+axy+y2是一个完全平方式，那么a的值应该是（　　）
A．8B．16C．-16D．16或-16

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网