题目内容
2. 如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
分析 过D作AB的平行线,交BC于E,交x轴于F,得出ABEF是矩形,根据矩形的性质得出EF=AB=3.由DE∥AB,根据平行线分线段成比例定理求出DE=$\frac{2}{3}$AB=2,则DF=1,即D点纵坐标为1,再根据反比例函数y=-$\frac{3}{x}$的图象经过点D,即可求出点D的横坐标.
解答  解:过D作AB的平行线,交BC于E,交x轴于F,则ABEF是矩形,EF=AB=3.
解:过D作AB的平行线,交BC于E,交x轴于F,则ABEF是矩形,EF=AB=3.
∵DE∥AB,CD=2AD,
∴$\frac{DE}{AB}$=$\frac{CD}{AC}$=$\frac{2}{3}$,
∴DE=$\frac{2}{3}$AB=2,
∴DF=EF-DE=3-2=1,
∴D点纵坐标为1,
∵反比例函数y=-$\frac{3}{x}$的图象经过点D,
∴y=1时,x=-3,
∴点D的横坐标是-3.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征,矩形的判定与性质,平行线分线段成比例定理,求出D点纵坐标是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
13.下列格式,运算正确的是( )
| A. | a6÷a2=a3 | B. | (-3a2)2=9a4 | C. | 3a+4b=7ab | D. | 2a-2=$\frac{1}{2{a}^{2}}$ |
10.不等式组$\left\{\begin{array}{l}{-2x+1<x+4}\\{\frac{x}{2}-\frac{x-1}{3}≤1}\end{array}\right.$的整数解( )个.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.某种衬衫的价格经过连续两次的降价后,由每件150元降到96元,则平均每次降价的百分率是( )
| A. | 10% | B. | 15% | C. | 20% | D. | 30% |

 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与△ABC相似的是( )
下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与△ABC相似的是( )



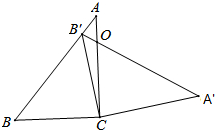 如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )