题目内容
12.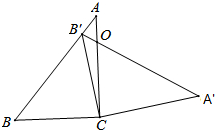 如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
分析 由三角形的内角和为180°可得出∠A=40°,由旋转的性质可得出BC=B′C,从而得出∠B=∠BB′C=50°,再依据三角形外角的性质结合角的计算即可得出结论.
解答 解:∵在三角形ABC中,∠ACB=90°,∠B=50°,
∴∠A=180°-∠ACB-∠B=40°.
由旋转的性质可知:
BC=B′C,
∴∠B=∠BB′C=50°.
又∵∠BB′C=∠A+∠ACB′=40°+∠ACB′,
∴∠ACB′=10°,
∴∠COA′=∠AOB′=∠OB′C+∠ACB′=∠B+∠ACB′=60°.
故选B.
点评 本题考查了旋转的性质、角的计算依据外角的性质,解题的关键是算出∠ACB′=10°.本题属于基础题,难度不大,解决该题型题目时,依据旋转的性质找出相等的角和相等的边,再通过角的计算求出角的度数是关键.

练习册系列答案
相关题目
2. 如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
 如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
3.父子二人并排垂站立于游泳池中时,爸爸露出水面的高度是他自身身高的$\frac{1}{3}$,儿子露出水面的高度是他自身身高的$\frac{1}{7}$,父子二人的身高之和为3.2米.若设爸爸的身高为x米,儿子的身高为y米,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{x+y=3.2}\\{(1+\frac{1}{7})x=(1+\frac{1}{3})y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=3.2}\\{(1-\frac{1}{7})x=(1-\frac{1}{3})y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=3.2}\\{\frac{1}{3}x=\frac{1}{7}y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=3.2}\\{(1-\frac{1}{3})x=(1-\frac{1}{7})y}\end{array}\right.$ |
7.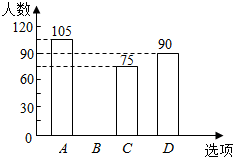 某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
请结合统计图表,回答下列问题:
(1)本次调查的学生共300人,a=10%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式恰好是“唱歌”和“舞蹈”的概率.
 某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:| 选项 | 方式 | 百分比 |
| A | 唱歌 | 35% |
| B | 舞蹈 | a |
| C | 朗诵 | 25% |
| D | 器乐 | 30% |
(1)本次调查的学生共300人,a=10%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式恰好是“唱歌”和“舞蹈”的概率.
17.超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是77.4分.
| 测试项目 | 创新能力 | 综合知识 | 语言表达 |
| 测试成绩(分数) | 70 | 80 | 92 |
4.下列说法中正确的是( )
| A. | “打开电视,正在播放《新闻联播》”是必然事件 | |
| B. | “x2<0(x是实数)”是随机事件 | |
| C. | 掷一枚质地均匀的硬币10次,可能有5次正面向上 | |
| D. | 为了了解夏季冷饮市场上冰淇淋的质量情况,宜采用普查方式调查 |
1.下列图形中,是轴对称图形但不是中心对称图形的是( )
| A. | 平行四边形 | B. | 等腰三角形 | C. | 矩形 | D. | 正方形 |
2.甲、乙两个搬运工搬运某种货物,已知乙比甲每小时多搬运600kg,甲搬运5000kg所用时间与乙搬运8000kg所用时间相等,求甲、乙两人每小时分别搬运多少kg货物,设甲每小时搬运xkg货物,则可列方程为( )
| A. | $\frac{5000}{x-600}=\frac{8000}{x}$ | B. | $\frac{5000}{x}=\frac{8000}{x+600}$ | C. | $\frac{5000}{x+600}=\frac{8000}{x}$ | D. | $\frac{5000}{x}=\frac{8000}{x-600}$ |
