题目内容
12.如图,在直角坐标系内,已知点A(-3,0),点B是点A关于y轴的对称点,线段CD在直线y=4上移动,且CD=6.(1)求点B的坐标和当四边形ABCD是菱形时点D的坐标;
(2)若四边形ABCD各内角的平分线相交形成四边形EFGH.求证:四边形EFGH是矩形;
(3)在(2)的条件下,探究运动过程中,四边形EFGH有可能为正方形吗?若有可能,求出此时点F的坐标,若不可能,说明理由.

分析 (1)根据关于y轴的对称的点的特点即可得到B(3,0),根据四边形的性质得到AD=AB=6,设D(x,4),过D作DM⊥AB于M,根据勾股定理列方程即可得到结论;
(2)根据平行线的性质得到∠ADC+∠DAB=180°,根据角平分线的定义得到∠ADF=$\frac{1}{2}$∠ADC,∠DAF=$\frac{1}{2}$∠DAB,求得∠EFG=90°,同理∠FEH=∠EHG=∠HGF=90°,于是得到四边形EFGH是矩形;
(3)运动过程中,四边形EFGH有可能为正方形,运动过程中,四边形ABCD是矩形时,四边形EFGH为正方形,如图2,根据角平分线的定义得到∠1=∠2=∠3=∠4=45°,推出△ADF,△AOE,△DNG是等腰直角三角形,根据等腰直角三角形的性质得到AF=DF,AE=DG,等量代换得到FE=FG,推出四边形EFGH是正方形,根据等腰直角三角形的性质即可得到结论.
解答  解:(1)∵点A(-3,0),点B是点A关于y轴的对称点,
解:(1)∵点A(-3,0),点B是点A关于y轴的对称点,
∴B(3,0),
当四边形ABCD是菱形时,AD=AB=6,
设D(x,4),
如图1,过D作DM⊥AB于M,
∴AM2+DM2=AD2,即(x+3)2+42=62,
解得:x=-3±2$\sqrt{5}$,
∴当四边形ABCD是菱形时,D(-3+2$\sqrt{5}$,4),或(-3-2$\sqrt{5}$,4);
(2)∵AB∥CD,
∴∠ADC+∠DAB=180°,
∵DG,AE分别平分∠CDA,∠DAB,
∴∠ADF=$\frac{1}{2}$∠ADC,∠DAF=$\frac{1}{2}$∠DAB,
∴∠ADF+DAF=$\frac{1}{2}$(∠ADC+∠DAB)=90°,
∴∠AFD=90°,
∴∠EFG=90°,同理∠FEH=∠EHG=∠HGF=90°,
∴四边形EFGH是矩形;
(3)运动过程中,四边形EFGH有可能为正方形,运动过程中,四边形ABCD是矩形时,四边形EFGH为正方形,
如图2,∵AE,DG分别平分∠DAB,∠ADC,
∴∠1=∠2=∠3=∠4=45°,
∴△ADF,△AOE,△DNG是等腰直角三角形,
∴AF=DF,AE=DG,
∴FE=FG,
∵四边形EFGH是矩形,
∴四边形EFGH是正方形,
过F作FP⊥AD与P,延长PF交EG于Q,则PQ⊥EG,
∴PF=$\frac{1}{2}$AD=2,FQ=PQ-PF═OA-PF=1,
∴F(-1,2).
点评 本题考查了平行四边形的性质,矩形的性质,正方形的判定和性质,菱形的性质,角平分线的定义,等腰直角三角形的判定和性质,勾股定理,关于y轴对称的点的特点,熟练掌握特殊四边形的性质是解题的关键.

| 老师在课堂上放手让学生提问和表达情况调查 | |||||
| 选项 | A | B | C | D | E |
| 内容 | 从不 | 很少 | 有时 | 常常 | 总是 |
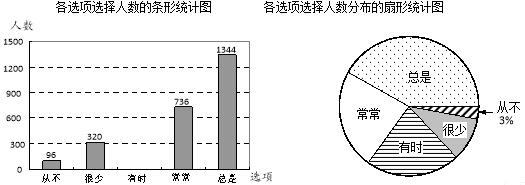
根据以上信息,解答下列问题:
(1)该区参加了本次问卷调查的八年级的学生共有多少名?
(2)请把这幅条形统计图补充完整.
(3)在扇形统计图中,“总是”所占的百分比多少?
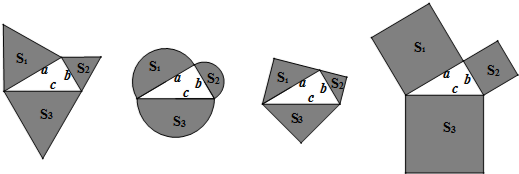
 如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )| A. | 22.5° | B. | 25° | C. | 23° | D. | 20° |
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
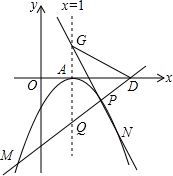 如图,已知直线y=kx+b(k>0)交抛物线y=-(x-1)2交于M、P两点,交抛物线对称轴x=1于Q(Q在x轴下方),交x轴于D,点N是点M关于对称轴x=1的对称点,延长NP交对称轴x=1于G,求证:DG=DQ.
如图,已知直线y=kx+b(k>0)交抛物线y=-(x-1)2交于M、P两点,交抛物线对称轴x=1于Q(Q在x轴下方),交x轴于D,点N是点M关于对称轴x=1的对称点,延长NP交对称轴x=1于G,求证:DG=DQ.
 如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )