题目内容
7.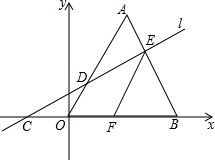 如图,在平面直角坐标系中,△A0B是边长为3的等边三角形,直线l与x轴、0A、AB分别交于点C、D、E,0C=AE.过点E作EF∥0A,交x轴于点F.
如图,在平面直角坐标系中,△A0B是边长为3的等边三角形,直线l与x轴、0A、AB分别交于点C、D、E,0C=AE.过点E作EF∥0A,交x轴于点F.(1)点A的坐标为:($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$);(结果保留根号)
(2)求证:点C、F关于y轴对称;
(3)若AD=EF.求直线l对应的函数表达式.
分析 (1)过点A作AM⊥x轴于点M,根据等边三角形的性质可知:AO=3、∠AOM=60°,在Rt△AMO中利用30°角的对边为斜边的一半结合勾股定理可求出AM、OM的长,从而得出点A的坐标;
(2)由EF∥0A利用平行线的性质可得出∠BFE=∠BOA=60°,结合∠OBA=60°可得出△BEF为等边三角形,根据等边三角形的性质即可得出BE=BF可得出BE=BF、BO=BA,进而即可得出AE=OF,再由OC=AE即可得出OC=OF,从而证出点C、F关于y轴对称;
(3)设OC=OF=x,根据边与边的关系找出∠OCD=∠ODC,再根据平行线的性质即可得出∠CEF=∠CDO=∠ECF,进而可得出CF=EF,由此即可得出关于x的一元一次方程,解方程即可求出x的值,进而可得出点C、D的坐标,利用待定系数法即可求出直线l对应的函数表达式.
解答 解:(1)过点A作AM⊥x轴于点M,如图1所示.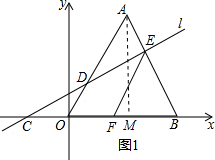
∵△A0B是边长为3的等边三角形,
∴AB=OB=OA=3,且∠AOM=60°.
在Rt△AMO中,OA=3,∠AOM=60°,
∴∠OAM=30°,
∴OM=$\frac{1}{2}$OA=$\frac{3}{2}$,AM=$\sqrt{O{A}^{2}-O{M}^{2}}$=$\frac{3\sqrt{3}}{2}$,
∴点A的坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).
故答案为:($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).
(2)证明:若证C、F关于y轴对称,只需证OC=OF即可.
∵EF∥OA,
∴∠BFE=∠BOA=60°,
∵∠OBA=60°,
∴△BEF为等边三角形,
∴BE=BF.
∵△AOB是等边三角形,
∴BO=BA,
∴AE=AB-BE=OB-BE=OF,
又∵0C=AE,
∴OC=OF.
∴点C、F关于y轴对称.
(3)设OC=OF=x,
∵OB=3,
∴BF=EF=3-x,
∵AD=EF,
∴AD=3-x.
∵OA=3,
∴OD=x,
∴∠OCD=∠ODC.
∵OA∥EF,
∴∠CEF=∠CDO=∠ECF,
∴EF=CF,即3-x=2x,
解得:x=1,
∴点C的坐标为(-1,0),点D的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
设直线l对应的函数表达式为y=kx+b,
将点C(-1,0)、点D($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)代入直线l对应的函数表达式中,
得$\left\{\begin{array}{l}{0=-k+b}\\{\frac{\sqrt{3}}{2}=\frac{1}{2}k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=\frac{\sqrt{3}}{3}}\end{array}\right.$.
故直线l对应的函数表达式为y=$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$.
点评 本题考查了等边三角形的性质、平行线的性质、解直角三角形以及待定系数法求函数解析式,解题的关键:(1)在Rt△AMO中求出AM、OM的长;(2)证出AE=OF;(3)求出点C、D的坐标.本题属于中档题,整体难度不大,解决该题型题目时,根据等边(等腰)三角形的性质找出相等的边,再通过30°角以及勾股定理找出各边长是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,直线y=2x+4与x,y轴分别交于点A,B,以OB为底边在y轴右侧作等腰△OBC,将点C向左平移4个单位,使其对应点C′恰好落在直线AB上,则点C的坐标为( )
如图,直线y=2x+4与x,y轴分别交于点A,B,以OB为底边在y轴右侧作等腰△OBC,将点C向左平移4个单位,使其对应点C′恰好落在直线AB上,则点C的坐标为( )| A. | (5,2) | B. | (4,2) | C. | (3,2) | D. | (-1,2) |
| A. | cos30° | B. | (-π)0 | C. | -$\frac{1}{3}$ | D. | $\sqrt{64}$ |
| A. | 互相垂直 | B. | 平行 | ||
| C. | 相交但不垂直 | D. | 平行或相交都有可能 |
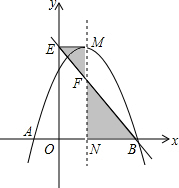 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F.
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F. 如图,△ABC三边的长分别为AB=4,BC=5,CA=6,直线l∥BC分别交△ABC的两边AB、AC于点M、N.
如图,△ABC三边的长分别为AB=4,BC=5,CA=6,直线l∥BC分别交△ABC的两边AB、AC于点M、N. 如图,直线y=x+b(b≠0)交坐标轴于A、B两点,交双曲线y=$\frac{2}{x}$于点D,从点D分别作两坐标轴的垂线DC、DE,垂足分别为C、E,连接BC、OD.
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,交双曲线y=$\frac{2}{x}$于点D,从点D分别作两坐标轴的垂线DC、DE,垂足分别为C、E,连接BC、OD.