题目内容
12. 如图,△ABC三边的长分别为AB=4,BC=5,CA=6,直线l∥BC分别交△ABC的两边AB、AC于点M、N.
如图,△ABC三边的长分别为AB=4,BC=5,CA=6,直线l∥BC分别交△ABC的两边AB、AC于点M、N.(1)若直线l平分△ABC的面积,则线段MN的长为$\frac{5\sqrt{2}}{2}$;
(2)若直线l过△ABC的内心I,试求MN的长为$\frac{10}{3}$.
分析 (1)由平行线的性质得出△AMN∽△ABC,由相似三角形的性质得出$\frac{MN}{BC}$=$\frac{\sqrt{2}}{2}$,即可求出MN的长;
(2)连接BI、CI,由平行线的性质解三角形的内心性质得出∠MIB=∠MBI,∠NIC=∠NCI,证出BM=IM,CN=IN,由平行线的性质得出△AMN∽△ABC,得出$\frac{AM}{MN}=\frac{AB}{BC}$=$\frac{4}{5}$,$\frac{AN}{MN}=\frac{AC}{BC}$=$\frac{6}{5}$,设AM=4a,则MN=5a,得出BM=4-4a,CN=6-6a,得出方程,解方程即可.
解答 解:(1)∵直线l平分△ABC的面积,
∴△ABC的面积=2△AMN的面积,
∵l∥BC,
∴△AMN∽△ABC,
∴$\frac{MN}{BC}$=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,
即$\frac{MN}{5}=\frac{\sqrt{2}}{2}$,
∴MN=$\frac{5\sqrt{2}}{2}$;
故答案为:$\frac{5\sqrt{2}}{2}$;
(2)连接BI、CI,如图所示:
∵MN∥BC,
∴∠MIB=∠IBC,∠NIC=∠ICB,
∵I为△ABC的内心,
∴∠MBI=∠IBC,∠NCI=∠ICB,
∴∠MIB=∠MBI,∠NIC=∠NCI,
∴BM=IM,CN=IN,
∵MN∥BC,
∴△AMN∽△ABC,
∴$\frac{AM}{MN}=\frac{AB}{BC}$=$\frac{4}{5}$,$\frac{AN}{MN}=\frac{AC}{BC}$=$\frac{6}{5}$,
设AM=4a,则MN=5a,
∴BM=4-4a,CN=6-6a,
∴5a=4-4a+6-6a,
解得:a=$\frac{2}{3}$,
∴MN=5×$\frac{2}{3}$=$\frac{10}{3}$;
故答案为:$\frac{10}{3}$.
点评 本题考查了三角形的内心性质、平行线的性质、相似三角形的判定与性质等知识;熟练掌握相似三角形的判定与性质是解决问题的关键.

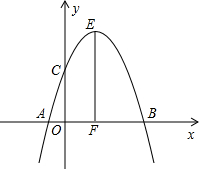 如图,抛物线y=-x2+2x+3经过点A、B、C,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,则实数m的变化范围为-$\frac{5}{4}$≤m≤5.
如图,抛物线y=-x2+2x+3经过点A、B、C,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,则实数m的变化范围为-$\frac{5}{4}$≤m≤5.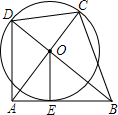 如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BO的延长线交⊙O于C、D.若⊙O的半径为1,求四边形ABCD的面积最小值.
如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BO的延长线交⊙O于C、D.若⊙O的半径为1,求四边形ABCD的面积最小值.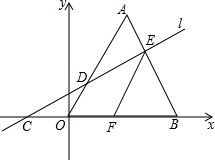 如图,在平面直角坐标系中,△A0B是边长为3的等边三角形,直线l与x轴、0A、AB分别交于点C、D、E,0C=AE.过点E作EF∥0A,交x轴于点F.
如图,在平面直角坐标系中,△A0B是边长为3的等边三角形,直线l与x轴、0A、AB分别交于点C、D、E,0C=AE.过点E作EF∥0A,交x轴于点F.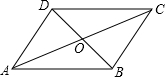 如图,在平行四边形ABCD中,O是对角线AC,BD的交点
如图,在平行四边形ABCD中,O是对角线AC,BD的交点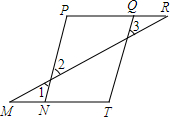 如图,M、N、T和A、B、C分别在同一直线上,且∠1=∠3,∠P=∠T,求证:PQ∥MT.
如图,M、N、T和A、B、C分别在同一直线上,且∠1=∠3,∠P=∠T,求证:PQ∥MT.