题目内容
15.先化简,再求值:($\frac{1}{a}$+$\frac{1}{b}$)÷$\frac{{a}^{2}+2ab+{b}^{2}}{a+b}$,其中a=-3,b=2.分析 先把括号内通分和除法运算化为乘法运算,再把分母因式分解后约分得到原式=$\frac{1}{ab}$,然后把a、b的值代入计算即可.
解答 解:原式=$\frac{a+b}{ab}$•$\frac{a+b}{(a+b)^{2}}$
=$\frac{1}{ab}$,
当a=-3,b=2时,原式=$\frac{1}{-3×2}$=-$\frac{1}{6}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
5.如图①,边长为a的大正方形中有四个边长均为b的小正方形,小华将阴影部分拼成了一个长方形(如图②),则这个长方形的面积为( )
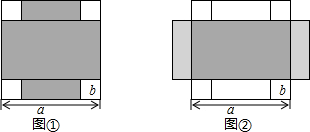

| A. | a2-4b2 | B. | (a+b)(a-b) | C. | (a+2b)(a-b) | D. | (a+b)(a-2b) |
4. 在如图所示的计算程序中,若输入x的值为-4.2,则输出的结果y为( )
在如图所示的计算程序中,若输入x的值为-4.2,则输出的结果y为( )
 在如图所示的计算程序中,若输入x的值为-4.2,则输出的结果y为( )
在如图所示的计算程序中,若输入x的值为-4.2,则输出的结果y为( )| A. | -4, | B. | 4 | C. | -5 | D. | 5 |
 沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:
沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论: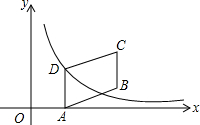 如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.
如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2. 如图,AO⊥CO,BO⊥DO,∠AOD=150°,则∠BOC的度数是30°.
如图,AO⊥CO,BO⊥DO,∠AOD=150°,则∠BOC的度数是30°.