题目内容
6.已知直线y=kx+b与y=-$\frac{1}{3}x+\frac{2}{3}$平行,且和直线y=-$\frac{2}{3}x+\frac{4}{3}$交于y轴上的同一点,求直线的解析式.分析 根据平行的性质设直线为$y=-\frac{1}{3}x+b$,根据直线y=-$\frac{2}{3}x+\frac{4}{3}$求得与y轴的交点坐标,代入即可求得b的值.
解答 解∵直线y=kx+b与$y=-\frac{1}{3}x+\frac{2}{3}$平行,
∴$k=-\frac{1}{3}$,则$y=-\frac{1}{3}x+b$
又∵直线$y=-\frac{2}{3}x+\frac{4}{3}$与y轴的交点为(0,$\frac{4}{3}$)
∴直线$y=-\frac{1}{3}x+b$与y轴也交于(0,$\frac{4}{3}$)
则 $\frac{4}{3}=-\frac{1}{3}×0+b$,即$b=\frac{4}{3}$
∴直线的解析式为$y=-\frac{1}{3}x+\frac{4}{3}$
点评 本题主要考查了两条直线平行或相交问题,根据一次函数的特点及两直线平行未知数系数的特点解答,难度一般.

练习册系列答案
相关题目
16.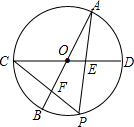 如图,AB,CD是⊙O的两条直径,∠AOC=120°,P是弧BD上的任意一点(不与点B,D重合),AP,CP分别交CD,AB于点E,F.若S△AOE+S△COF=2$\sqrt{3}$,则⊙O的半径为( )
如图,AB,CD是⊙O的两条直径,∠AOC=120°,P是弧BD上的任意一点(不与点B,D重合),AP,CP分别交CD,AB于点E,F.若S△AOE+S△COF=2$\sqrt{3}$,则⊙O的半径为( )
 如图,AB,CD是⊙O的两条直径,∠AOC=120°,P是弧BD上的任意一点(不与点B,D重合),AP,CP分别交CD,AB于点E,F.若S△AOE+S△COF=2$\sqrt{3}$,则⊙O的半径为( )
如图,AB,CD是⊙O的两条直径,∠AOC=120°,P是弧BD上的任意一点(不与点B,D重合),AP,CP分别交CD,AB于点E,F.若S△AOE+S△COF=2$\sqrt{3}$,则⊙O的半径为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
16.下列方程中,有实数根的是( )
| A. | x2-3x+5=0 | B. | $\sqrt{x-2}+1=0$ | C. | $\sqrt{x+2}=-x$ | D. | $\frac{x}{{{x^2}-1}}=\frac{1}{{{x^2}-1}}$ |
 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.