题目内容
5.先化简($\frac{1}{x-1}-x+1$)$÷\frac{2x-{x}^{2}}{{x}^{2}-1}$,然后从-3≤x≤3的范围内选取一个合适的整数作为x的值代入求值.分析 先把括号内通分和除法运算化为乘法运算,再把分子分母因式分解,然后约分得到原式=x+1,再根据分式有意义的条件把x=3代入计算即可.
解答 解:原式=$\frac{1-(x-1)^{2}}{x-1}$•$\frac{(x+1)(x-1)}{-x(x-2)}$
=$\frac{-x(x-2)}{x-1}$•$\frac{(x+1)(x-1)}{-x(x-2)}$
=x+1,
当x=3时,原式=3+1=4.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
16.下列方程中,有实数根的是( )
| A. | x2-3x+5=0 | B. | $\sqrt{x-2}+1=0$ | C. | $\sqrt{x+2}=-x$ | D. | $\frac{x}{{{x^2}-1}}=\frac{1}{{{x^2}-1}}$ |
15.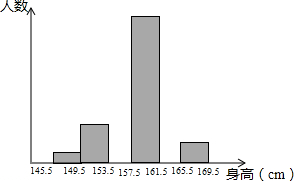 为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
(1)中m和n表示的数分别是多少?
(2)将如表中的数据画成频数分布直方图.
(3)如果全校有2500名女生,则身高在161.5cm以上的约有多少人?
 为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)(1)中m和n表示的数分别是多少?
(2)将如表中的数据画成频数分布直方图.
(3)如果全校有2500名女生,则身高在161.5cm以上的约有多少人?
| 组别 | 人数 | 百分比 |
| 145.5~149.5 | 1 | 2% |
| 149.5~153.5 | 4 | 8% |
| 153.5~157.5 | m | 40% |
| 157.5~161.5 | 15 | 30% |
| 161.5~165.5 | 8 | n |
| 165.5~169.5 | 2 | 4% |
| 合计 | 50 | 100% |
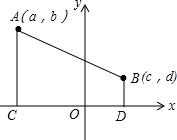 已知,如图,点A(a,b),B(c,d)在平面直角坐标系中的任意两点,且AC⊥x轴于点C,BD⊥x轴于点D.
已知,如图,点A(a,b),B(c,d)在平面直角坐标系中的任意两点,且AC⊥x轴于点C,BD⊥x轴于点D.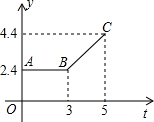 如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.