题目内容
13.若正比例函数y=kx(k≠0)与反比例函数y=$\frac{a}{x}$(a≠0)的图象有两个交点,其中一个交点的坐标为(-3,-2),则另一个交点的坐标为( )| A. | (2,3) | B. | (3,-2) | C. | (-2,3) | D. | (3,2) |
分析 根据正比例函数与反比例函数的交点关于原点对称进行解答即可.
解答 解:∵正比例函数和反比例函数均关于原点对称,
∴两函数的交点关于原点对称,
∵一个交点的坐标是(-3,-2),
∴另一个交点的坐标是(3,2),
故选D.
点评 本题考查的是正比例函数与反比例函数的交点问题,熟知正比例函数与反比例函数的交点关于原点对称的知识是解答此题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
4.把直线y=-x-3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m的取值范围是( )
| A. | 1<m<7 | B. | 3<m<4 | C. | m>1 | D. | m<4 |
8.化简:
(1)$\frac{1}{{2+\sqrt{3}}}$;
(2)$10\sqrt{\frac{1}{5}}+\frac{5}{2}\sqrt{\frac{4}{5}}-\sqrt{45}$.
(1)$\frac{1}{{2+\sqrt{3}}}$;
(2)$10\sqrt{\frac{1}{5}}+\frac{5}{2}\sqrt{\frac{4}{5}}-\sqrt{45}$.
2.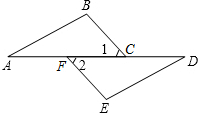 如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的是( )
如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的是( )
 如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的是( )
如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的是( )| A. | ∠E=∠B | B. | ED=BC | C. | AB=EF | D. | AF=CD |
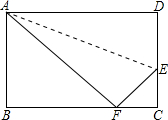 如图,在长方形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,若点D恰好落在BC上的F处,且△ABF的面积是30,求DE的长.
如图,在长方形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,若点D恰好落在BC上的F处,且△ABF的面积是30,求DE的长. 如图,某登山运动员从营地A沿坡度为1:$\sqrt{3}$的斜坡AB到达山顶B,如果AB=1000米,则他实际上升了500米.
如图,某登山运动员从营地A沿坡度为1:$\sqrt{3}$的斜坡AB到达山顶B,如果AB=1000米,则他实际上升了500米.