题目内容
1.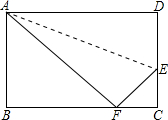 如图,在长方形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,若点D恰好落在BC上的F处,且△ABF的面积是30,求DE的长.
如图,在长方形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,若点D恰好落在BC上的F处,且△ABF的面积是30,求DE的长.
分析 利用△ABF的面积求得BF的长,然后利用勾股定理得到AF的长,由折叠的性质知,EF=DE,AD=AF,结合Rt△EFC中,CF2+CE2=EF2,即可解得EF的值,进而求得DE.
解答 解:∵△ABF的面积为30cm2,AB=DC=5cm
∴BF=12(cm).
∴AF=13(cm),
∵EF=DE,AD=AF=13(cm),
∴CF=BC-BF=13-12=1(cm).
在Rt△EFC中
CF2+CE2=EF2即12+(5-EF)2=EF2
∴EF=2.6cm.
则DE=EF=2.6(cm).
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13.若正比例函数y=kx(k≠0)与反比例函数y=$\frac{a}{x}$(a≠0)的图象有两个交点,其中一个交点的坐标为(-3,-2),则另一个交点的坐标为( )
| A. | (2,3) | B. | (3,-2) | C. | (-2,3) | D. | (3,2) |
 如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴
如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴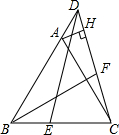 如图,已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E.∠ABC的平分线BF,交CD于点F,过点A作AH⊥CD于H.当∠EDC=30°,CF=$\frac{4}{3}$,则DH=$\frac{2}{3}$.
如图,已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E.∠ABC的平分线BF,交CD于点F,过点A作AH⊥CD于H.当∠EDC=30°,CF=$\frac{4}{3}$,则DH=$\frac{2}{3}$. 如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则FD的长为( )
如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则FD的长为( )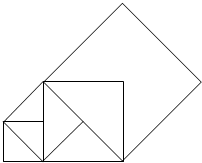 如图,先画一个边长为1的正方形,以其对角线为边画第二个正方形,再以第二个正方形的对角线为边画第三个正方形,…,如此反复下去,那么第n个正方形的对角线长为($\sqrt{2}$)n.
如图,先画一个边长为1的正方形,以其对角线为边画第二个正方形,再以第二个正方形的对角线为边画第三个正方形,…,如此反复下去,那么第n个正方形的对角线长为($\sqrt{2}$)n.