题目内容
5.认真阅读以下材料,并解答问题:材料:(1)配方:利用完全平方公式,把二次三项式写成(a-k)2+h的形式.
例:x2-2x=x2-2•1•x+12-12=(x-1)2-1
(2)利用配方法解方程ax2+bx+c=0(a≠0)
问题:(1)把多项式直接写成(a-k)2+h的形式:x2-6x-3=(x-3)2-12
(2)用配方法解方程:x2+6x+8=0.
分析 材料:(2)把二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,左边配成完全平方的形式,如果右边的式子为非负数,就可以两边直接开平方求出方程的根.
问题:(1)根据配方法的步骤,直接配方即可;
(2)先移项,再进行配方,然后进行计算即可.
解答 解:∵a≠0,
∴两边同时除以a得:x2+$\frac{b}{a}$x+$\frac{c}{a}$=0,
x2+$\frac{b}{a}$x=-$\frac{c}{a}$,
x2+$\frac{b}{a}$x+$\frac{{b}^{2}}{4{a}^{2}}$=$\frac{{b}^{2}}{4{a}^{2}}$-$\frac{c}{a}$,
(x+$\frac{b}{2a}$)2=$\frac{{b}^{2}-4ac}{4{a}^{2}}$,
∵a≠0,
∴4a2>0,
当b2-4ac≥0时,两边直接开平方有:
x+$\frac{b}{2a}$=±$\frac{\sqrt{{b}^{2}-4ac}}{2a}$,
x=--$\frac{b}{2a}$±$\frac{\sqrt{{b}^{2}-4ac}}{2a}$,
∴x1=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$,x2=$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$;
当b2-4ac<0时,此方程无实数根.
问题:(1)x2-6x-3=x2-2•3x+32-32-3=(x-3)2-12,
故答案为(x-3)2-12;
(2)解方程:x2+6x+8=0.
x2+6x=-8
x2+6x+9=9-8
(x+3)2=1
∴x+3=±1,
∴x1=-2,x2=-4.
点评 此题考查了配方法的应用,解题时要注意配方法的步骤,注意在变形的过程中不要改变式子的值,若二次项系数为1,则常数项是一次项系数的一半的平方,若二次项系数不为1,则可先提取二次项系数,将其化为1后再计算.

 如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.
如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.| A. | 3 | B. | 6 | C. | 8 | D. | $\sqrt{17}$-1 |
| A. | (2,3) | B. | (3,-2) | C. | (-2,3) | D. | (3,2) |
| A. |  | B. |  | C. |  | D. |  |
 如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则FD的长为( )
如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则FD的长为( ) 如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第6块.
如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第6块.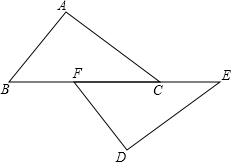 已知如图,点B、F、C、E、在一条直线上,AB⊥AC,DE⊥DF,AC=DF,BF=CE.求证:AB∥DE.
已知如图,点B、F、C、E、在一条直线上,AB⊥AC,DE⊥DF,AC=DF,BF=CE.求证:AB∥DE.