题目内容
3．
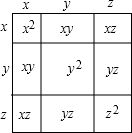如图，通过计算大正方形的面积，可以验证一个等式，这个等式是（ ）| A． | （x+y+z）2=x2+y2+z2+2y+xz+yz | B． | （x+y+z）2=x2+y2+z+2xy+xz+2yz | ||
| C． | （x+y+z）2=x2+y2+z2+2xy+2xz+2yz | D． | （x+y+z）2=（x+y）2+2xz+2yz |
分析 根据大长方形的面积=3个正方形的面积+6个小长方形的面积，即可解答．
解答 解：根据题意得：
（x+y+z）2=x2+y2+z2+2xy+2xz+2yz，
故选：C．
点评 本题考查了完全平方公式的几何背景，解决本题的关键是明确大长方形的面积=3个正方形的面积+6个小长方形的面积．
练习册系列答案
相关题目
12．下列一元二次方程中，没有实数根的是（ ）
| A． | x2+x-1=0 | B． | 2x2+2x+1=0 | C． | x2-2$\sqrt{3}$x+3=0 | D． | x2+6x=-5 |
