题目内容

18．已知实数x、y满足$\sqrt{2x-16}+|x-2y+4|=0$，求2x-$\frac{4}{3}y$的立方根．

分析 先依据非负数的性质求得x、y的值，然后再求得代数式的值，最后再求得它的立方根即可．

解答 解：由非负数的性质可知：2x-16=0，x-2y+4=0，
解得：x=8，y=6．
∴2x-$\frac{4}{3}$y=2×8-$\frac{4}{3}$×6=8．
∴2x-$\frac{4}{3}y$的立方根是2．

点评 本题主要考查的是非负数的性质、立方根的定义，求得x、y的值是解题的关键．

练习册系列答案
相关题目
8．如图，四边形ABCD中，∠A=100°，∠C=70°，点M、N分别在AB、BC上，将△BMN沿MN翻折，得△FMN．若MF∥AD，FN∥DC，则∠B的度数为95°．
9．计算：|-$\frac{1}{2}$|-2-1-（π-4）0．
6．60°补角的度数是120度．
13．【背景介绍】勾股定理是几何学中的明珠，充满着魅力．千百年来，人们对它的证明趋之若骛，其中有著名的数学家，也有业余数学爱好者．向常春在1994年构造发现了一个新的证法．
【小试牛刀】把两个全等的直角三角形如图1放置，其三边长分别为a、b、c．显然，∠DAB=∠B=90°，AC⊥DE．请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积，再探究这三个图形面积之间的关系，可得到勾股定理：
S梯形ABCD=$\frac{1}{2}$a（a+b），S△EBC=$\frac{1}{2}$b（a-b），S四边形AECD=$\frac{1}{2}$c2，
则它们满足的关系式为$\frac{1}{2}$a（a+b）=$\frac{1}{2}$b（a-b）+$\frac{1}{2}$c2，经化简，可得到勾股定理．
【知识运用】（1）如图2，铁路上A、B两点（看作直线上的两点）相距40千米，C、D为两个村庄（看作两个点），AD⊥AB，BC⊥AB，垂足分别为A、B，AD=25千米，BC=16千米，则两个村庄的距离为41千米（直接填空）；

（2）在（1）的背景下，若AB=40千米，AD=24千米，BC=16千米，要在AB上建造一个供应站P，使得PC=PD，请用尺规作图在图2中作出P点的位置并求出AP 的距离．
【知识迁移】借助上面的思考过程与几何模型，求代数式$\sqrt{{x^2}+9}+\sqrt{{{（16-x）}^2}+81}$的最小值（0＜x＜16）
3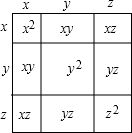．如图，通过计算大正方形的面积，可以验证一个等式，这个等式是（　　）
A．（x+y+z）2=x2+y2+z2+2y+xz+yzB．（x+y+z）2=x2+y2+z+2xy+xz+2yz
C．（x+y+z）2=x2+y2+z2+2xy+2xz+2yzD．（x+y+z）2=（x+y）2+2xz+2yz
10．如图所示，AB∥CD，∠A=128°，∠D=32°，求∠AED的度数．
7．如图，平行四边形ABCD中，点O是AC与BD的交点，过点O的直线与BA，DC的延长线分别交于点E，F．
（1）求证：△AOE≌△COF；
（2）连接EC，AF，求证：四边形AECF是平行四边形．
8．如图所示的几何体是由5个大小相同的小正方体紧密摆放而成的，其三视图中面积最小的是（　　）
A．主视图B．左视图C．俯视图D．左视图和俯视图

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网