题目内容
12.下列一元二次方程中,没有实数根的是( )| A. | x2+x-1=0 | B. | 2x2+2x+1=0 | C. | x2-2$\sqrt{3}$x+3=0 | D. | x2+6x=-5 |
分析 分别求得每个选项中的根的判别式的值,找到b2-4ac<0的即为本题的正确的选项.
解答 解:A、∵△=1-4×1×(-1)=9>0,∴方程有两个不相等的实数根,故本选项错误;
B、∵△=4-4×2×1=-4<0,∴方程没有实数根,故本选项正确;
C、∵△=12-4×1×3=0,∴方程有两个相等的实数根,故本选项错误;
D、∵△=36-4×1×5=56>0,∴方程有两个不相等的实数根,故本选项错误;
故选B.
点评 本题考查了根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0时,方程有两个不相等的实数根;
(2)△=0时,方程有两个相等的实数根;
(3)△<0时,方程没有实数根.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
3.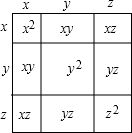 如图,通过计算大正方形的面积,可以验证一个等式,这个等式是( )
如图,通过计算大正方形的面积,可以验证一个等式,这个等式是( )
 如图,通过计算大正方形的面积,可以验证一个等式,这个等式是( )
如图,通过计算大正方形的面积,可以验证一个等式,这个等式是( )| A. | (x+y+z)2=x2+y2+z2+2y+xz+yz | B. | (x+y+z)2=x2+y2+z+2xy+xz+2yz | ||
| C. | (x+y+z)2=x2+y2+z2+2xy+2xz+2yz | D. | (x+y+z)2=(x+y)2+2xz+2yz |
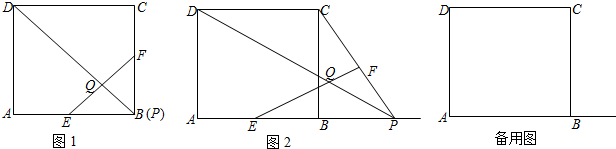
 如图,平行四边形ABCD中,点O是AC与BD的交点,过点O的直线与BA,DC的延长线分别交于点E,F.
如图,平行四边形ABCD中,点O是AC与BD的交点,过点O的直线与BA,DC的延长线分别交于点E,F. 如图,在平面直角坐标系中,□ABCO的顶点A、C的坐标分别为A (2,0)、C (-1,2),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B.
如图,在平面直角坐标系中,□ABCO的顶点A、C的坐标分别为A (2,0)、C (-1,2),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B. 如图,已知直线y1=-$\frac{1}{2}$x+1与x轴交于点A,与直线y2=-$\frac{3}{2}$x交于点B.
如图,已知直线y1=-$\frac{1}{2}$x+1与x轴交于点A,与直线y2=-$\frac{3}{2}$x交于点B.