题目内容
12．已知x1，x2是一元二次方程x2-4x+1=0的两个根．求：（1）（x1-3）（x2-3）的值；
（2）（x1-x2）2的值．
分析 根据根与系数的关系得到x1+x2=4，x1x2=1，再利用完全平方公式和通过把原式变形得到结果．
解答 解：∵x1，x2是一元二次方程x2-4x+1=0的两个实数根，
∴x1+x2=4，x1x2=1，
∴（1）（x1-3）（x2-3）=x1x2-3（x1+x2）+9=1-3×4+9=-2；
（2）（x1-x2）2=（x1+x2）2-4x1x2=16-4=12．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．也考查了代数式的变形能力．
练习册系列答案
相关题目
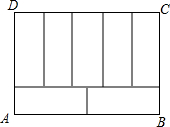如图，周长为68cm的长方形ABCD被分成7个相同的矩形，求长方形ABCD的面积．
如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．