题目内容
3.开封市大力发展足球进校园活动,某校在去年购买A,B两种足球,费用分别为2400元和2000元,其中A种足球数量是B种足球数量的2倍,两种足球一共买30个.(1)求A,B两种足球的单价;
(2)由于该校今年被定为“足球特色校”,学校决定再次购买A,B两种足球共18个,本次购买B种足球的数量不少于A种足球数量的2倍,若单价不变,则本次如何购买能使费用W最少?
分析 (1)设A种足球单价为x元,则B足球单价为y元,根据:A种足球个数=2×B种足球个数,A种足球个数+B种足球个数=30,列方程组求解即可;
(2)设再次购买A种足球x个,则B种足球为(18-x)个,购买总费用为W,根据:总费用=A种足球单价×A种足球数量+B种足球单价×B种足球数量,列出W关于x的函数关系式,由B种足球的数量不少于A种足球数量的2倍可得x的范围,继而根据一次函数性质可得最值情况.
解答 解:(1)A种足球单价为x元,则B足球单价为y元,根据题意得:
$\left\{\begin{array}{l}{\frac{2400}{x}=\frac{2000}{y}×2}\\{\frac{2400}{x}+\frac{2000}{y}=30}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=120}\\{y=200}\end{array}\right.$,
经检验:$\left\{\begin{array}{l}{x=120}\\{y=200}\end{array}\right.$是方程组的解.
答:A种足球单价为120元,B足球单价为200元.
(2)设再次购买A种足球x个,则B种足球为(18-x)个,
根据题意得:W=120x+200(18-x)=-80x+3600,
∵18-x≥2x,
∴x≤6,
∵-80<0,
∴W随x的增大而减小,
∴当x=6时,W最小,此时18-x=12.
答:本次购买A种足球6个,B种足球12个,才能使购买费用W最少.
点评 本题主要考查二元一次方程组的应用与一次函数的实际应用能力,根据题意找到相等关系并据此列出方程或函数关系式是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
14.有一天A、B两家文具店卖同样的自动铅笔和笔记本的销售情况如下:
根据信息,求自动铅笔和笔记本的单价.
| 自动铅笔(单位:支) | 笔记本(单位:本) | 总销售额(元) | |
| A | 20 | 32 | 72 |
| B | 10 | 36 | 56 |
13.小李有2根木棒,长度分别为10cm和15cm,要组成一个三角形(木棒的首尾分别相连接),第三根木棒的长为( )
| A. | 4cm | B. | 5cm | C. | 20cm | D. | 25cm |
 直线a、b、c、d的位置如图所示,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于55度.
直线a、b、c、d的位置如图所示,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于55度. 如图,直角梯形ABCD中,∠A=∠B=∠DEC=90°,E为AB中点,求证:AD+BC=DC.
如图,直角梯形ABCD中,∠A=∠B=∠DEC=90°,E为AB中点,求证:AD+BC=DC.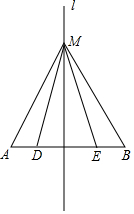 如图所示,l是AB的中垂线,M是l上一点,D,E是AB上不同的两点,则AM=BM吗?MD=ME吗?
如图所示,l是AB的中垂线,M是l上一点,D,E是AB上不同的两点,则AM=BM吗?MD=ME吗? 如图,已知△ABC的两边AB,AC的垂直平分线相交于点O,求证:点O在边BC的垂直平分线上.
如图,已知△ABC的两边AB,AC的垂直平分线相交于点O,求证:点O在边BC的垂直平分线上.