题目内容
17.在直角坐标系中有两个点D(1,-3),E(-1,-4),在y轴上确定一个点Q,使Q到D,E的距离和最短,求Q点的坐标.分析 如图,连接DE交y轴于Q,则此时,Q到D,E的距离和最短,设直线DE的解析式为:y=kx+b,解方程组即可得到结论.
解答  解:如图,连接DE交y轴于Q,
解:如图,连接DE交y轴于Q,
则此时,Q到D,E的距离和最短,
设直线DE的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{-3=k+b}\\{-4=-k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-\frac{7}{2}}\end{array}\right.$,
∴直线DE的解析式为:y=$\frac{1}{2}$x-$\frac{7}{2}$,
当x=0时,y=-$\frac{7}{2}$,
∴Q(0,-$\frac{7}{2}$).
点评 本题考查轴对称-最短问题、坐标与图形变化-对称、两点之间线段最短等知识,解题的关键是理解轴对称的定义,学会利用对称解决最短问题,属于中考常考题型.

练习册系列答案
相关题目
6.星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
| 进价(元/个) | 售价(元/个) | |
| 电饭煲 | 200 | 250 |
| 电压锅 | 160 | 200 |
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
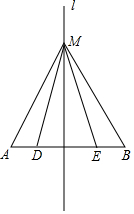 如图所示,l是AB的中垂线,M是l上一点,D,E是AB上不同的两点,则AM=BM吗?MD=ME吗?
如图所示,l是AB的中垂线,M是l上一点,D,E是AB上不同的两点,则AM=BM吗?MD=ME吗?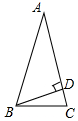 如图,等腰△ABC中,∠ABC=∠ACB,BD为AC边上的高.
如图,等腰△ABC中,∠ABC=∠ACB,BD为AC边上的高.