题目内容
4. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.(1)求证:CE=AD;
(2)填空:
①当AB=2BE时,四边形BECD是菱形;
②在①的基础上,当∠A的度数为45°时,四边形BECD是正方形.
分析 (1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;
(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;
(3)当∠A=45°,四边形BECD是正方形.
解答 (1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:AB=2BE时,四边形BECD是菱形,
理由是:∵四边形BECD是菱形,
∴CE=EB=BD,
∵CE=AD,
∴BD=CE,
∴AD=BD,
∴AB=2BE.
故答案是:2;
(3)当∠A=45°时,∵∠ACB=90°,
∴∠ABC=45°,
由(2)可知,四边形BECD是菱形,
∴∠ABC=∠CBE=45°,
∴∠DBE=90°,
∴四边形BECD是正方形.
故答案是:45°.
点评 本题考查了平行四边形的性质和判定,菱形的判定,正方形的判定、直角三角形的性质的应用,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
14.有一天A、B两家文具店卖同样的自动铅笔和笔记本的销售情况如下:
根据信息,求自动铅笔和笔记本的单价.
| 自动铅笔(单位:支) | 笔记本(单位:本) | 总销售额(元) | |
| A | 20 | 32 | 72 |
| B | 10 | 36 | 56 |
16. 用四个完全一样的长方形(长、宽分别设为x、y)拼成如图所示的大正方形,已知大正方形的面积为36,中间空缺的小正方形的面积为4,则下列关系式中不正确的是( )
用四个完全一样的长方形(长、宽分别设为x、y)拼成如图所示的大正方形,已知大正方形的面积为36,中间空缺的小正方形的面积为4,则下列关系式中不正确的是( )
 用四个完全一样的长方形(长、宽分别设为x、y)拼成如图所示的大正方形,已知大正方形的面积为36,中间空缺的小正方形的面积为4,则下列关系式中不正确的是( )
用四个完全一样的长方形(长、宽分别设为x、y)拼成如图所示的大正方形,已知大正方形的面积为36,中间空缺的小正方形的面积为4,则下列关系式中不正确的是( )| A. | x+y=6 | B. | x2+y2=36 | C. | x•y=8 | D. | x-y=2 |
13.小李有2根木棒,长度分别为10cm和15cm,要组成一个三角形(木棒的首尾分别相连接),第三根木棒的长为( )
| A. | 4cm | B. | 5cm | C. | 20cm | D. | 25cm |
14.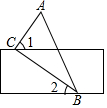 如图,将直尺和直角三角板ABC按如图方式摆放,已知∠ACB=90°,∠1=65°,则∠2的大小是( )
如图,将直尺和直角三角板ABC按如图方式摆放,已知∠ACB=90°,∠1=65°,则∠2的大小是( )
 如图,将直尺和直角三角板ABC按如图方式摆放,已知∠ACB=90°,∠1=65°,则∠2的大小是( )
如图,将直尺和直角三角板ABC按如图方式摆放,已知∠ACB=90°,∠1=65°,则∠2的大小是( )| A. | 35° | B. | 30° | C. | 25° | D. | 20° |
 如图,已知△ABC的两边AB,AC的垂直平分线相交于点O,求证:点O在边BC的垂直平分线上.
如图,已知△ABC的两边AB,AC的垂直平分线相交于点O,求证:点O在边BC的垂直平分线上. 如图,已知:AB∥CD∥EF,OC:CE=2:3,OA:OD=3:2,OB=6cm,OD=4cm.求线段BE、AF的长.
如图,已知:AB∥CD∥EF,OC:CE=2:3,OA:OD=3:2,OB=6cm,OD=4cm.求线段BE、AF的长.