题目内容
2.解下列方程组:(1)$\left\{\begin{array}{l}{x+y=9}\\{3(x+y)+2x=33}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y+1}{3}=1}\\{3x+2y=10}\end{array}\right.$.
分析 (1)方程组整理后,利用代入消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)方程组整理得:$\left\{\begin{array}{l}{x+y=9①}\\{3(x+y)+2x=33②}\end{array}\right.$,
①代入②得:27+2x=33,
解得:x=3,
把x=3代入①得:y=6,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=6}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{3x-2y=8①}\\{3x+2y=10②}\end{array}\right.$,
①+②得:6x=18,
解得:x=3,
把x=3代入①得:y=$\frac{1}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=\frac{1}{2}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
12.若等腰三角形中有一个角等于70°,则这个等腰三角形的顶角的度数是( )
| A. | 70° | B. | 40° | C. | 70°或40° | D. | 70°或55° |
 如图,一拱桥呈抛物线状,桥的最大高度是16m,跨度是40m,求在线段AB上离中心M处15m的地方,桥的高度是多少?
如图,一拱桥呈抛物线状,桥的最大高度是16m,跨度是40m,求在线段AB上离中心M处15m的地方,桥的高度是多少?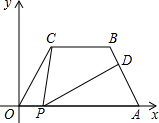 如图所示,在平面直角坐标系中,四边形OABC中BC∥OA,∠COP=∠BAO=60°,OC=AB=4,OA=7,点P为x轴上一个动点,点P不与点O、点A重合.连接CP,过点P作PD交AB于点D.
如图所示,在平面直角坐标系中,四边形OABC中BC∥OA,∠COP=∠BAO=60°,OC=AB=4,OA=7,点P为x轴上一个动点,点P不与点O、点A重合.连接CP,过点P作PD交AB于点D.
 小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度.
小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度. 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,∠ABD与∠C互补.
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,∠ABD与∠C互补.