Question

7．如图，已知∠AOB=45°，画射线OC⊥OA，射线OD⊥OB，画出所有可能的情形并分别求出∠COD的度数．

Answer 1

分析 分OC、OD在边OA的同侧和异侧分别作出图形，然后分别进行计算即可得解．

解答 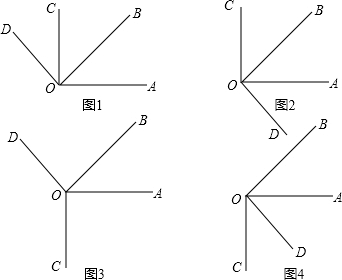解：分四种情况：
如图1，∵OC⊥OA，OD⊥OB，
∴∠AOB+∠BOC=90°，∠COD+∠BOC=90°，
∴∠COD=∠AOB=45°；

如图2，∵OC⊥OA，OD⊥OB，
∴∠AOC=∠BOD=90°，
∠BOC=∠AOC-∠AOB=90°-45°=45°，
∴∠COD=∠BOD+∠BOC=90°+45°=135°；

如图3，∠COD=360°-∠AOC-∠AOB-∠BOD，
=360°-90°-45°-90°，
=135°；

如图4，∵OC⊥OA，OD⊥OB，
∴∠AOB+∠AOD=90°，∠COD+∠AOD=90°，
∴∠COD=∠AOB=45°．
综上所述，∠COD的度数为45°或135°．

点评 本题考查了垂线的定义，角的计算，同角的余角相等的性质的综合应用，解题的难点在于分情况讨论．