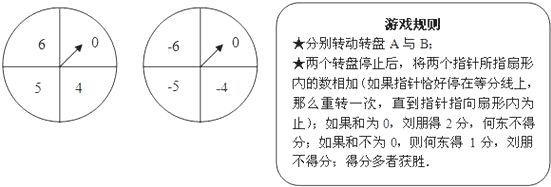
题目内容
6．用直接开平方法解下列方程：（1）（x-3）2=16；
（2）3（x+1）2=$\frac{1}{3}$．
分析 （1）两边开方，即可得出两个一元一次方程，求出方程的解即可；
（2）两边都除以3，再开方，即可得出两个一元一次方程，求出方程的解即可．
解答 解：（1）（x-3）2=16，
x-2=±4，
x1=6，x2=-2；
（2）3（x+1）2=$\frac{1}{3}$，
（x+1）2=$\frac{1}{9}$，
x+1=±$\frac{1}{3}$，
x1=-$\frac{2}{3}$，x2=-1$\frac{1}{3}$．
点评 本题考查了解一元二次方程的应用，解此题的关键是能把一元二次方程转化成一元一次方程，难度适中．
练习册系列答案
阅读快车系列答案
相关题目
16．
将n个边长都为1cm的正方形按如图所示的方法摆放，点A1，A2，…，An分别是正方形对角线的交点，则n个正方形重叠形成的重叠部分的面积和为（ ）
将n个边长都为1cm的正方形按如图所示的方法摆放，点A1，A2，…，An分别是正方形对角线的交点，则n个正方形重叠形成的重叠部分的面积和为（ ）| A． | $\frac{1}{4}$ cm2 | B． | $\frac{n-1}{4}$cm2 | C． | $\frac{n}{4}$ cm2 | D． | （$\frac{1}{4}$）ncm2 |
14．某中学矩形了一次演讲比赛，分段统计参赛同学的成绩，结果如表所示（分数为整数，满分为100分）：
则这次演讲比赛的同学的平均数为77分～86分．
| 分数段（分） | 61～70 | 71～80 | 81～90 | 91～100 |
| 人数（人） | 2 | 8 | 6 | 4 |
1．
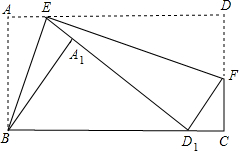已知矩形ABCD中，AB=4，AD=7，点E是边AD上的点，点F是边DC上的点，分别沿BE，EF折叠得得到点A1，D1，恰好使D1落在BC上，且E，A1，D1同线，AE＞2，则AE=（ ）
已知矩形ABCD中，AB=4，AD=7，点E是边AD上的点，点F是边DC上的点，分别沿BE，EF折叠得得到点A1，D1，恰好使D1落在BC上，且E，A1，D1同线，AE＞2，则AE=（ ）| A． | $\frac{7}{3}$ | B． | $\frac{8}{3}$ | C． | $\frac{9}{4}$ | D． | $\frac{5}{2}$ |
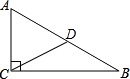如图所示，在△ABC中，∠ACB=90°，BC=5cm，AC=10cm，CD为中线，以点C为圆心，以$\frac{5}{2}$$\sqrt{5}$cm为半径作圆，则点A，B，D与⊙C的位置关系如何．
15．
如图，AC是矩形ABCD的对角线，⊙O是△ABC的内切圆，现将矩形ABCD按如图所示的方式折叠，使点D与点O重合，折痕为FG．点F，G分别在边AD，BC上，连结OG，DG．若OG⊥DG，且⊙O的半径长为1，则下列结论不成立的是（ ）
如图，AC是矩形ABCD的对角线，⊙O是△ABC的内切圆，现将矩形ABCD按如图所示的方式折叠，使点D与点O重合，折痕为FG．点F，G分别在边AD，BC上，连结OG，DG．若OG⊥DG，且⊙O的半径长为1，则下列结论不成立的是（ ）| A． | CD+DF=4 | B． | CD-DF=2$\sqrt{3}$-3 | C． | BC+AB=2$\sqrt{3}$+4 | D． | BC-AB=2 |
