题目内容
18.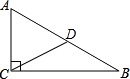 如图所示,在△ABC中,∠ACB=90°,BC=5cm,AC=10cm,CD为中线,以点C为圆心,以$\frac{5}{2}$$\sqrt{5}$cm为半径作圆,则点A,B,D与⊙C的位置关系如何.
如图所示,在△ABC中,∠ACB=90°,BC=5cm,AC=10cm,CD为中线,以点C为圆心,以$\frac{5}{2}$$\sqrt{5}$cm为半径作圆,则点A,B,D与⊙C的位置关系如何.
分析 根据勾股定理求出CD的值,根据点与圆的位置关系特点,判断即可.
解答 解:在△ABC中,∠ACB=90°,BC=5cm,AC=10cm,
∴AB=$\sqrt{{AC}^{2}+B{C}^{2}}$=5$\sqrt{5}$,
∵CD为中线,
∴CD=$\frac{1}{2}$AB=$\frac{5\sqrt{5}}{2}$,
∵AC=10cm>$\frac{5}{2}$$\sqrt{5}$cm,
∴点A在⊙C的外面,
∵BC=5cm<$\frac{5}{2}$$\sqrt{5}$cm,
∴点B在⊙C的内部,
∵CD=$\frac{5\sqrt{5}}{2}$,
∴点D在⊙C上.
点评 本题考查了点与圆的位置关系,解题的关键是确定圆的半径和点与圆心之间的距离之间的大小关系.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
7.孝感市2014年生产总值约136800000000元,数据136800000000用科学记数法表示为( )
| A. | 1.368×10 | B. | 13.68×1010 | C. | 1.368×1011 | D. | 1.368×1012 |

 如图,D、E、F分别是△ABC的AB、AC、BC上的中点,若AB=7,BC=6,AC=5,则△DEF的周长是9.
如图,D、E、F分别是△ABC的AB、AC、BC上的中点,若AB=7,BC=6,AC=5,则△DEF的周长是9.