题目内容
14．某中学矩形了一次演讲比赛，分段统计参赛同学的成绩，结果如表所示（分数为整数，满分为100分）：| 分数段（分） | 61～70 | 71～80 | 81～90 | 91～100 |
| 人数（人） | 2 | 8 | 6 | 4 |
分析 首先求出参加这次演讲比赛的同学的人数；然后用总分数段的最小值和最大值分别除以参加这次演讲比赛的同学的人数，求出这次演讲比赛的同学的平均数的范围即可．
解答 解：这次演讲比赛的同学的人数为：
2+8+6+4=20（人）；
∵（61×2+71×8+81×6+91×4）÷20
=1540÷20
=77（分）
（70×2+80×8+90×6+100×4）÷20
=1720÷20
=86（分）
∴这次演讲比赛的同学的平均数为77分～86分．
故答案为：77分～86分．
点评 此题主要考查了加权平均数的含义和求法的应用，要熟练掌握，解答此题的关键是要明确：对于一组不同权重的数据，加权平均数更能反映数据的真实信息．
练习册系列答案
中考解读考点精练系列答案
相关题目
4．观察下列图形，阅读图形下面的相关文字，
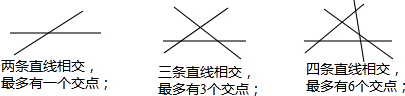
（1）填空
（2）当若干条直线相交时，设最多交点个数为m，对顶角对数为n，则m与n有何关系？
（1）填空
| 直线条数 | 最多交点个数 | 对顶角的对数 |
| 2 | 1 | 2 |
| 3 | 3 | 6 |
| 4 | 6 | 12 |
| 5 | 10 | 20 |
| … | … | … |
| n | $\frac{n（n-1）}{2}$ | n（n-1） |
5．
如图的立体图形是由四个相同的小正方体组成，它的主视图是（ ）
如图的立体图形是由四个相同的小正方体组成，它的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
已知，如图，扇形AOD的半径为4，A，B，C，D是弧上四点，且AB=BC=CD=2，则AD的长度=5.5．
19．$\sqrt{\frac{y}{x}}$+$\sqrt{\frac{x}{y}}$=$\frac{3\sqrt{2}}{2}$，那么$\frac{y}{x}$+$\frac{x}{y}$的值等于（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{5}{2}$ | C． | $\frac{7}{2}$ |