题目内容
6.适合下列条件的△ABC的三边a、b、c,不能组成直角三角形的是( )| A. | a=3,b=3,c=3$\sqrt{2}$ | B. | a=7,b=24,c=25 | C. | a=8,b=15,c=17 | D. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ |
分析 根据直角三角形的判定,符合a2+b2=c2即可;反之不符合的不能构成直角三角形.
解答 解:A、因为32+32=(3$\sqrt{2}$)2,所以能组成直角三角形;
B、因为72+242=252,所以能组成直角三角形;
C、因为82+152=172,所以能组成直角三角形;
D、因为($\frac{1}{4}$)2+($\frac{1}{5}$)2≠($\frac{1}{3}$)2,所以不能组成直角三角形;
故选D.
点评 本题考查了直角三角形的判定,运用勾股定理的逆定理判定是解答此题的关键.

练习册系列答案
相关题目
5. 如图,在菱形ABCD中,下列结论中错误的是( )
如图,在菱形ABCD中,下列结论中错误的是( )
 如图,在菱形ABCD中,下列结论中错误的是( )
如图,在菱形ABCD中,下列结论中错误的是( )| A. | ∠1=∠2 | B. | AC⊥BD | C. | AB=AD | D. | AC═BD |
18.如果直角三角形的三条边为3、4、a,则a的取值可以有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
15.一个直角三角形的两条直角边边长分别为3和4,则斜边上的高为( )
| A. | 2 | B. | 2.2 | C. | 2.4 | D. | 2.5 |
 如图是一辆汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数图象.
如图是一辆汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数图象. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,CD⊥AB于点D.动点P从点A出发,沿A→C 以1cm/s的速度向终点C运动,点P不与A、C重合.过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边向PQ右侧作正方形PQMN.设正方形PQMN与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,CD⊥AB于点D.动点P从点A出发,沿A→C 以1cm/s的速度向终点C运动,点P不与A、C重合.过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边向PQ右侧作正方形PQMN.设正方形PQMN与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).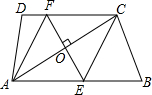 如图,在四边形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB,CD于点E,F,连接CE,AF.
如图,在四边形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB,CD于点E,F,连接CE,AF. 如图,正方形ABCD中,E、F分别是BC、CD的中点,连接AE、BF交于G,将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,将得到△AHM,AM和BF相交于点N.当正方形ABCD的面积为4时,则四边形GHMN的面积为$\frac{1}{5}$.
如图,正方形ABCD中,E、F分别是BC、CD的中点,连接AE、BF交于G,将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,将得到△AHM,AM和BF相交于点N.当正方形ABCD的面积为4时,则四边形GHMN的面积为$\frac{1}{5}$.