题目内容
4. 如图是一辆汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数图象.
如图是一辆汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数图象.(1)汽车在DE段行驶了1.5小时;
(2)汽车在BC段停留了0.5小时;
(3)汽车出发1小时时,离出发地多少千米?
分析 (1)由DE段图象对应时间t的值可知;
(2)由BC段图象对应时间t的值可知;
(3)待定系数求得AB段解析式,令t=1求得对应s的值.
解答 解:(1)汽车在DE段行驶时间为:4.5-3=1.5(小时),
故答案为:1.5;
(2)汽车在BC段停留时间为:2-1.5=0.5(小时),
故答案为:0.5;
(3)由图象可设AB段图象的函数表达式为y=kx,
当x=1.5时,y=80;
解得:k=$\frac{160}{3}$,
即y=$\frac{160}{3}$x,(0≤x≤1.5),
当x=1时,y=$\frac{160}{3}$,
答:行驶1小时时,离出发地$\frac{160}{3}$千米.
点评 本题主要考查一次函数的图象及待定系数法求函数解析式,读懂函数图象及其横纵轴的实际意义是解题的关键.

练习册系列答案
相关题目
9.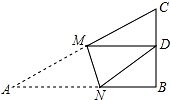 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )| A. | 4 | B. | 5 | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
16.用配方法解方程x2+6x+1=0时,原方程应变形为( )
| A. | (x+3)2=2 | B. | (x-3)2=2 | C. | (x+3)2=8 | D. | (x-3)2=8 |
6.适合下列条件的△ABC的三边a、b、c,不能组成直角三角形的是( )
| A. | a=3,b=3,c=3$\sqrt{2}$ | B. | a=7,b=24,c=25 | C. | a=8,b=15,c=17 | D. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ |
 如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )