题目内容
7.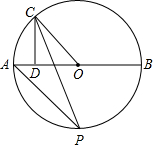 如图,AB为⊙O的直径,C为⊙O上半圆一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于点P,则当点C在⊙O上运动时,点P的位置( )
如图,AB为⊙O的直径,C为⊙O上半圆一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于点P,则当点C在⊙O上运动时,点P的位置( )| A. | 随点C的运动而改变 | B. | 不变 | ||
| C. | 在是PA=OA的劣弧上 | D. | 无法确定 |
分析 连OP,由CP平分∠OCD,得到∠1=∠2,而∠1=∠3,所以有OP∥CD,则OP⊥AB,即可得到OP平分半圆APB.
解答  解:连OP,如图,
解:连OP,如图,
∵CP平分∠OCD,
∴∠1=∠2,
而OC=OP,有∠1=∠3,
∴∠2=∠3,
∴OP∥CD,
又∵弦CD⊥AB,
∴OP⊥AB,
∴OP平分半圆APB,即点P是半圆的中点.
故选B.
点评 本题考查的是垂径定理及圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.也考查了垂径定理的推论.

练习册系列答案
相关题目
16.下列三条线段能构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,$\sqrt{2}$,2 | C. | $\sqrt{3}$,3,6 | D. | 6,8,10 |
 如图,直线a是一个轴对称图形的对称轴,画出这个轴对称图形的另一半,并说明这个轴对称图形是一个什么图形,它一共有几条对称轴.
如图,直线a是一个轴对称图形的对称轴,画出这个轴对称图形的另一半,并说明这个轴对称图形是一个什么图形,它一共有几条对称轴. 如图,AD是△ABC的角平分线,∠B=50°,∠ADC=70°,求∠BAC、∠C的度数.
如图,AD是△ABC的角平分线,∠B=50°,∠ADC=70°,求∠BAC、∠C的度数.




 已知:如图,△ABC中,∠C=90°,∠B的平分线交AC于点D,CD=15,AD=25,求AB的长.
已知:如图,△ABC中,∠C=90°,∠B的平分线交AC于点D,CD=15,AD=25,求AB的长.