题目内容
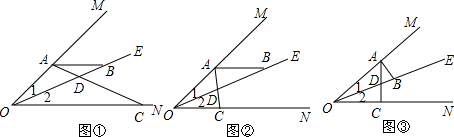
17.已知∠MON=40°,OE平分∠MON,点A、B在射线OM、OE上,点C是射线ON上的一个动点,连接AC交射线OE于点D,设∠OAC=x.(1)填空:若AB∥ON,
①当∠BAD=∠ABD时,(如图①),则x的度数为120°;
②当∠BAD=∠BDA时,(如图②),则x的度数为60°;
(2)若AB⊥OM于点A(如图③),且△ADB是等腰三角形,求x的度数.
分析 (1)①先根据角平分线的性质求出∠2的度数,再由平行线的性质即可得出结论;
②先由∠BAD=∠BDA,∠ABO=20°得出∠BAD=80°,再根据三角形内角和定理即可得出∠OAC的度数;
(2)分当点D在线段OB上,点D在射线BE上两种情况进行讨论.
解答 解:(1)①∵∠MON=40°,OE平分∠MON,
∴∠1=∠2=20°.
∵AB∥ON,∠BAD=∠ABD,
∴∠BAD=20°.
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=120°
②∵∠BAD=∠BDA,∠ABO=20°,
∴∠BAD=80°.
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=60°.
故答案为:120°,60°;
(2)①当点D在线段OB上时,
若∠BAD=∠ABD,则x=20°;
若∠BAD=∠BDA,则x=35°;
若∠ADB=∠ABD,则x=50°.
②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=125°.
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,且x=20°、35°、50°、125°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
相关题目
8.在△ABC中,若∠A:∠B:∠C=4:3:1,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 无法确定 |
5.菱形的面积为32cm2,一个内角是30°,则这个菱形的周长为( )
| A. | 24cm | B. | 28cm | C. | 30cm | D. | 32cm |
12.下列说法中,错误的是( )
| A. | 对角线相等的平行四边形是矩形 | |
| B. | 对角线平分对角的平行四边形是菱形 | |
| C. | 四个内角相等的四边形是矩形 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |
9.-$\frac{1}{2}$的倒数,相反数分别是( )
| A. | 2,2 | B. | -2,$\frac{1}{2}$ | C. | $\frac{1}{2}$,$\frac{1}{2}$ | D. | -$\frac{1}{2}$,-2 |
7.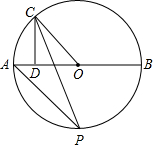 如图,AB为⊙O的直径,C为⊙O上半圆一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于点P,则当点C在⊙O上运动时,点P的位置( )
如图,AB为⊙O的直径,C为⊙O上半圆一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于点P,则当点C在⊙O上运动时,点P的位置( )
 如图,AB为⊙O的直径,C为⊙O上半圆一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于点P,则当点C在⊙O上运动时,点P的位置( )
如图,AB为⊙O的直径,C为⊙O上半圆一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于点P,则当点C在⊙O上运动时,点P的位置( )| A. | 随点C的运动而改变 | B. | 不变 | ||
| C. | 在是PA=OA的劣弧上 | D. | 无法确定 |
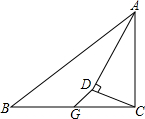 在△ABC中,AD平分∠BAC,CD⊥AD,D为垂足,G为BC的中点,求证:∠DGC=∠B.
在△ABC中,AD平分∠BAC,CD⊥AD,D为垂足,G为BC的中点,求证:∠DGC=∠B.